题目内容
16.已知⊙0的半径为13cm,弦AB=10cm,则圆心到弦AB的距离为12cm.此时弦AB把⊙O分成两个弓形,则这两个弓形的高分别为1cm和25cm.分析 过O作直径OC⊥AB于D,连接OA,则CD是弓形的高或DE是弓形的高,根据垂径定理求出AD,根据勾股定理求出圆心到弦AB的距离OD,进而即可求得两个弓形的高CD和DE.
解答 解:过O作直径OC⊥AB于D,连接OA,则CD是弓形的高或DE是弓形的高,
∵AB=10cm,
∴AD=$\frac{1}{2}$AB=5cm.
在Rt△OAD中,132=52+OD2,
得:OD=12,即圆心O到弦AB的距离为12cm.
∴CD=13cm-12cm=1cm,DE=13cm+12cm=25cm.
故答案为12cm,1cm和25cm.
点评 本题考查了垂径定理和勾股定理的应用,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.a,b表示两个负数,且|a|>|b|,则a与b的大小关系是( )
| A. | a>b | B. | a<b | C. | a=b | D. | 无法确定 |
7.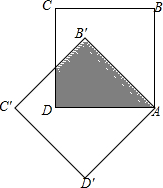 将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
 将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )
将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′,若图中阴影部分面积为$\sqrt{2}$+1,则x的值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
3.在△ABC中,已知a=1,b=1,c=$\sqrt{3}$,则∠C=( )
| A. | 120° | B. | 30° | C. | 45° | D. | 60° |
1.若x2+mxy+4y2是完全平方式,则常数m的值为( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 以上结果都不对 |
 如图,△ABC与△AEF中,AB=AE,BC=EF,AC=AF,AB交EF于D,求证:DA•DB=DE•DF.
如图,△ABC与△AEF中,AB=AE,BC=EF,AC=AF,AB交EF于D,求证:DA•DB=DE•DF.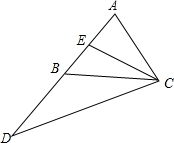 如图,在△ABC中,AC=AB,CE是AB边上的中线,延长AB至D,使BD=AB,问CE与CD有何数量关系?请说明理由.
如图,在△ABC中,AC=AB,CE是AB边上的中线,延长AB至D,使BD=AB,问CE与CD有何数量关系?请说明理由.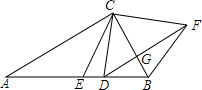 已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.
已知:△ABC中,∠ACB=90°,CE是中线,D是AB上的-点,过D作DF∥AC,过B作BF∥EC,DF、BF相交于F.连结CD、CF,求证:CD=CF.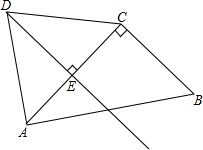 四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.
四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.