Question

7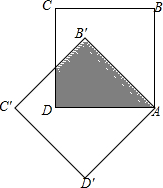．将边长为$\sqrt{2}$+1的正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′，若图中阴影部分面积为$\sqrt{2}$+1，则x的值为（　　）

• A． 30°
• B． 45°
• C． 60°
• D． 75°

Answer 1

分析 CD与C′B′相交于E，连结AE，如图，根据旋转的性质得∠BAB′=x，AB=AB′=AD，∠B′=∠B=90°，再利用”HL“证明Rt△AB′E≌Rt△ADE，则S_△ADE=$\frac{1}{2}$S_阴影=$\frac{1}{2}$（$\sqrt{2}$+1），∠B′AE=∠DAE，利用三角形面积公式可计算出DE=1，所以tan∠DAE=$\frac{DE}{AD}$=$\sqrt{2}$-1，所以∠DAE=22.5°，则∠DAB′=45°，即可得到∠BAB′=45°．

解答 解：CD与C′B′相交于E，连结AE，如图，
∵正方形ABCD绕点A逆时针旋转x度至正方形AB′C′D′，
∴∠BAB′=x，AB=AB′=AD，∠B′=∠B=90°，
在Rt△AB′E和Rt△ADE中，
$\left\{\begin{array}{l}{AE=AE}\\{AB′=AD}\end{array}\right.$，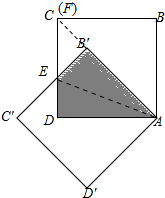
∴Rt△AB′E≌Rt△ADE，
∴S_△ADE=$\frac{1}{2}$S_阴影=$\frac{1}{2}$（$\sqrt{2}$+1），∠B′AE=∠DAE，
∵S_△ADE=$\frac{1}{2}$DE•AD，
∴$\frac{1}{2}$DE•（$\sqrt{2}$+1）=$\frac{1}{2}$（$\sqrt{2}$+1），解得DE=1，
延长AB′交CD于点F，设B′F=t，
则S_阴影=S_△ADF-S_△EB′F
∴$\sqrt{2}$+1=$\frac{1}{2}$（$\sqrt{2}$+1）（EF+1）-$\frac{1}{2}$t，
∴EF=（$\sqrt{2}$+1）t+1
∵△EB′F∽△ADF，
∴$\frac{EB′}{AD}=\frac{B′F}{DF}$，
∴t=1，即B′F=1，
∴∠DAB′=45°，
故选B．

点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．