题目内容
20.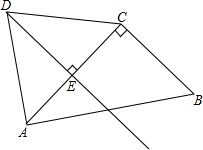 四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.
四边形ABCD中,AD=CD,AB=15,AC=12,BC=9,∠ACB=90°.(1)求△ABC的周长;
(2)过点D作DE⊥AC,垂足为E,点P是射线DE上的动点.设DP=x.
①求四边形BCDP的面积(用含x的代数式表示);
②△PBC的周长是否存在最小值?若存在求出它的最小值;若不存在请说明理由.
分析 (1)三角形的周长等于各边长之和;
(2)①先证明DE∥BC,然后利用等腰三角形三线合一的性质证明AE=CE,最后利用梯形的面积公式求解即可;②先证明DE是AC的垂直平分线,故此可知PC=PA,当点A、P、B在同一条直线上时,三角形的周长有最小值,最小值=BC+AB.
解答 解:(1)△ABC的周长=AB+BC+AC=15+9+12=36;
(2)①∵DE⊥AC,BC⊥AC,
∴DE∥BC.
∵AD=CD,DE⊥AC,
∴AE=EC=6.
由梯形的面积公式可知:四边形BCDP的面积=$\frac{1}{2}(PD+BC)•EC$=$\frac{1}{2}×(x+9)×6$=3x+27;
②如图所示:
∵DE⊥AC,AE=EC,
∴DE是AC的垂直平分线.
∴PC=PA.
△PCB的周长=BC+PB+PC=BC+PB+PA.
由两点直线线段最短可知:当点A、P、B在一条直线上时,AP+PB有最小值.
∴△PCB的周长的最小值=BC+AB=6+15=21.
点评 本题主要考查的是等腰三角形的性质、线段垂直平分线的性质和判定、两点之间线段最短,明确当点A、P、B在一条直线上时三角形的周长有最小值是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
15.一个四边形截去一个内角后变为( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 以上均有可能 |
15.正方形的面积y与边长x之间的函数关系的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列说法正确的是( )
| A. | 若|a|=-a,则a<0 | |
| B. | $-\frac{3}{2}π{x^2}y$的系数是$-\frac{3}{2}$ | |
| C. | 一个有理数与它的相反数之积一定不大于0 | |
| D. | 多项式3xy2-4x3y+12的次数为7 |
 小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?
小华早晨从家出发匀速步行上学,小华在已步行200米时,爷爷发现小华的眼镜忘在家里,随即出发步行送眼镜去学校.小华到学校后发现眼镜未带上,立即原路返回,途中与爷爷相遇,如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图,则小华家到学校的距离为多少米?