题目内容
5. 如图,A、B是⊙O上两点,有下列四种寻找$\widehat{AB}$的中点C的方法:
如图,A、B是⊙O上两点,有下列四种寻找$\widehat{AB}$的中点C的方法:①连接OA、OB,作∠AOB的角平分线交$\widehat{AB}$于点C;
②连接AB,作OH⊥AB于H,交$\widehat{AB}$于点C;
③在优弧$\widehat{AmB}$上取一点D,作∠ADB的平分线交$\widehat{AB}$于点C;
④分别过A、B作⊙O的切线,两切线交于点P,连接OP交$\widehat{AB}$于点C.
其中正确的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
分析 根据圆心角、弧、弦的关系对①进行判断;根据垂径定理对②进行判断;根据圆周角定理对③进行判断;如图3,先根据切线长定理和切线的性质得OP平分∠APB,OA⊥AP,OB⊥PB,则利用等角的余角相等得到∠AOC=∠BOC,然后根据圆心角、弧、弦的关系可对④进行判断.
解答 解:作∠AOB的角平分线交$\widehat{AB}$于点C,如图1,
则∠AOC=∠BOC,所以$\widehat{AC}$=$\widehat{BC}$,所以①正确;
如图1,∵OH⊥AB于H,
∴$\widehat{AC}$=$\widehat{BC}$,所以②正确;
如图2,∵∠ADC=∠BDC,
所以$\widehat{AC}$=$\widehat{BC}$,所以③正确;
如图3,
∵PA、PB为⊙O的切线,
∴OP平分∠APB,OA⊥AP,OB⊥PB,
∴∠AOC=∠BOC,
∴$\widehat{AC}$=$\widehat{BC}$,所以④正确.
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了垂径定理和圆心角、弧、弦的关系.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
11.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 垂直于同一条直线的两条直线互相平行 |
17.一个三角形的三个内角之比是2:3:4,则此三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 以上三种都有可能 |
 是由五个大小相同的小方块拼凑而成的,问:
是由五个大小相同的小方块拼凑而成的,问: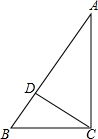 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$