题目内容
17．若一个正多边形的周长是63，且内角和1260°，则它的边长为7．分析 先根据多边形的内角和公式求出多边形的边数，再用周长63除以边数求解即可．
解答 解：设多边形的边数是n，则
（n-2）•180°=1260°，
解得n=9，
∵多边形的各边相等，
∴它的边长是：63÷9=7．
故答案为：7．
点评 主要考查了多边形的内角和公式，熟记公式求出多边形的边数是解题的关键．
练习册系列答案
相关题目
8．对于反比例函数y=$\frac{3}{x}$，当x＞1时，y的取值范围是（ ）
| A． | 0＜y＜3 | B． | y＞3或y＜0 | C． | y＞3 | D． | 以上答案都错 |
5．在①平行四边形，②矩形，③菱形，④正方形中，既是轴对称图形，又是中心对称图形的是（ ）
| A． | ①②③④ | B． | ②③ | C． | ②③④ | D． | ①③④ |
如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
2．如图①，在平面直角坐标系中，平行四边形ABCD在第一象限，AB∥x轴，直线y=-x从原点出发沿x轴正方向平移，被平行四边形ABCD截得的线段EF的长度m与平移的距离s的函数图象如图②所示，那么平行四边形ABCD的面积为（ ）
| A． | 8$\sqrt{2}$ | B． | 12 | C． | 4$\sqrt{2}$ | D． | 6 |
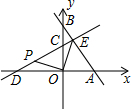如图，在平面直角坐标系xOy中，直线y=-$\frac{4}{3}$x+4分别与x轴、y轴交于A、B两点，直线y=kx+3分别与x轴、y轴交于D、C两点，且CD=AB．
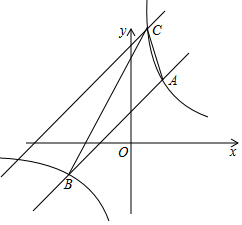如图，在平面直角坐标系中，直线y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于点A（2，m）、B（-4，-2），其中k1≠0，k2＞0．