Question

7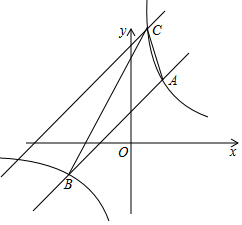．如图，在平面直角坐标系中，直线y₁=k₁x+b的图象与反比例函数y₂=$\frac{{k}_{2}}{x}$的图象分别交于点A（2，m）、B（-4，-2），其中k₁≠0，k₂＞0．
（1）求m的值和直线的解析式；
（2）若y₁＞y₂，观察图象，请直接写出x的取值范围；
（3）将直线y₁=k₁x+b的图象向上平移与反比例函数的图象在第一象限内交于点C，C点的横坐标为1，求△ABC的面积．

Answer 1

分析 （1）把A（2，m）、B（-4，-2）代入反比例函数解析式，即可得到m=4，k₂=8，把A（2，4）、B（-4，-2）代入直线y₁=k₁x+b，可得直线AB的解析式；
（2）根据直线在双曲线上方部分所有的点的横坐标，即可得到x的取值范围；
（3）过C作CD∥y轴，交AB于D，求得C（1，8），D（1，3），即可得出CD=8-3=5，再根据S_△ABC=S_△ACD+S_△BCD进行计算即可．

解答 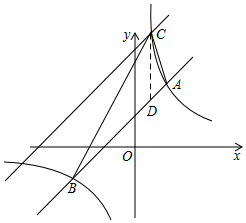解：（1）把A（2，m）、B（-4，-2）代入反比例函数y₂=$\frac{{k}_{2}}{x}$，可得
k₂=2m=-4×（-2），
∴m=4，k₂=8，
把A（2，4）、B（-4，-2）代入直线y₁=k₁x+b，可得
$\left\{\begin{array}{l}{4=2{k}_{1}+b}\\{-2=-4{k}_{1}+b}\end{array}\right.$，
解得k₁=1，b=2，
∴直线AB的解析式为：y₁=x+2；

（2）由图可得，若y₁＞y₂，则-4＜x＜0或x＞2；

（3）过C作CD∥y轴，交AB于D，
∵C点的横坐标为1，
∴当x=1时，y=$\frac{8}{1}$=8，即C（1，8），
当x=1时，y₁=1+2=3，即D（1，3），
∴CD=8-3=5，
又∵A（2，4）、B（-4，-2），
∴S_△ABC=S_△ACD+S_△BCD=$\frac{1}{2}$×5×1+$\frac{1}{2}$×5×5=15．

点评 本题主要考查了反比例函数与一次函数交点问题，从函数的角度看，就是寻求使一次函数值大于（或小于）反比例函数值的自变量x的取值范围；从函数图象的角度看，就是确定直线在双曲线上方（或下方）部分所有的点的横坐标所构成的集合．