题目内容
2.如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,AB∥x轴,直线y=-x从原点出发沿x轴正方向平移,被平行四边形ABCD截得的线段EF的长度m与平移的距离s的函数图象如图②所示,那么平行四边形ABCD的面积为( )
| A. | 8$\sqrt{2}$ | B. | 12 | C. | 4$\sqrt{2}$ | D. | 6 |
分析 根据图象可以得到当移动的距离是4时,直线经过点A,当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,当直线经过D点,设交AB与N,则DN=4,作DM⊥AB于点M.利用三角函数即可求得DM,即平行四边形的高,然后利用平行四边形的面积公式即可求解.
解答  解:解据图象可以得到当移动的距离是4时,直线经过点A,
解:解据图象可以得到当移动的距离是4时,直线经过点A,
当移动距离是7时,直线经过D,在移动距离是8时经过B,则AB=8-4=4,
当直线经过D点,设交AB与N,则DN=4,
作DM⊥AB于点M.
∵y=-x与x轴形成的角是45°,
又∵AB∥x轴,
∴∠DNM=45°,
∴DM=DN•sin45°=4×$\frac{\sqrt{2}}{2}$=2$\sqrt{2}$,
∴平行四边形的面积=AB•DM=4×2$\sqrt{2}$=8$\sqrt{2}$.
故选:A.
点评 本题考查了函数的图象,根据图象理解AB的长度,运用解直角三角形求得平行四边形的高是解决问题的关键.

练习册系列答案
相关题目
7.在某次救灾过程中,需要向A、B两个机场分别运送100吨和70吨生活物资,已知该物资在甲仓库存有90吨,乙仓库存有80吨,若从甲、乙两仓库运动物资到机场的费用(元/吨)如表所示:
(1)设从甲仓库运送到A机场的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)请设计并说明总运费最低时的调配方案,并求出这时的最低费用.
| 机场 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A机场 | 15 | 20 |
| B机场 | 10 | 8 |
(2)请设计并说明总运费最低时的调配方案,并求出这时的最低费用.
11.一次函数y=3x-6的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
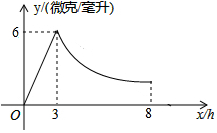 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.
某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度(微克/毫升)与服药后时间x(时)之间的函数关系如图所示,当血液中药物浓度上升时,y与x成正比,下降时,y与x成反比.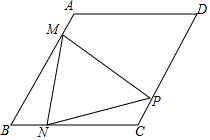 在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.