题目内容
7．如果抛物线y=-2x2+bx+3的对称轴是x=1，那么b=4．分析 由抛物线的对称轴是直线x=1，可得出$\frac{b}{4}$=1，解之即可得出b值．
解答 解：∵抛物线y=-2x2+bx+3的对称轴是直线x=1，
∴-$\frac{b}{2×（-2）}$=$\frac{b}{4}$=1，
解得：b=4．
点评 本题考查了二次函数的性质，牢记“二次函数y=ax2+bx+c（a≠0）的对称轴是直线x=-$\frac{b}{2a}$”是解题的关键．
练习册系列答案
相关题目
11．
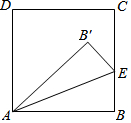如图，将正方形ABCD的一角折叠，折痕为AE，∠B′AD比∠B′AE大48°，设∠B′AE和∠B′AD的度数分别为x、y，那么x、y所适合的一个方程组是（ ）
如图，将正方形ABCD的一角折叠，折痕为AE，∠B′AD比∠B′AE大48°，设∠B′AE和∠B′AD的度数分别为x、y，那么x、y所适合的一个方程组是（ ）| A． | $\left\{\begin{array}{l}y-x=48\\ y+x=90\end{array}\right.$ | B． | $\left\{\begin{array}{l}y-x=48\\ y=2x\end{array}\right.$ | C． | $\left\{\begin{array}{l}y-x=48\\ y+2x=90\end{array}\right.$ | D． | $\left\{\begin{array}{l}x-y=48\\ y+2x=90\end{array}\right.$ |
12．在平面直角坐标系中，若点A （a，-b）在第一象限内，则点B （a，b-3）所在的象限是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
2．已知正比例函数y=kx的图象经过点（1，-2），若A（x1，y1），B（x2，y2）是正比例函数图象上的两点，且满足x1+x2=1，则y1+y2的值为（ ）
| A． | -2 | B． | $-\frac{3}{2}$ | C． | -1 | D． | 0 |
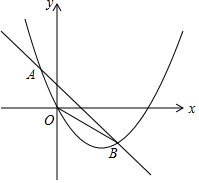如图，在平面直角坐标系中，抛物线y=x2-bx与直线交于点A（-$\frac{1}{2}$，m），B（1，n），其中m＞0，n＜0，
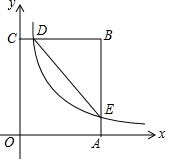如图，在矩形OABC中，OA=3，OC=5，分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y=$\frac{k}{x}$（k＞0）的图象经过点D且与边BA交于点E，连接DE．