题目内容
8.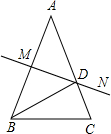 如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.
如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.(1)求∠DBC的度数;
(2)求△BCD的周长.
分析 ①先求出∠ABD,再用直角三角形的性质,计算即可.
②直接等量代换求出周长即可.
解答 解:∵AB=AC=8,∠A=40°,
∴∠ABC=∠C=70°
∵AB边的中垂线MN交AC于点D,
∴AD=BD,∠ABD=∠A=40°,
①由(1)得,∠ABD=40°,∠ABC=70°,
∴∠DBC=∠ABC-∠ABD=70°-40°=30°,
②△BCD的周长=BC+CD+DB=BC+(CD+DB)=BC+AC=5+8=13.
点评 此题是等腰三角形的性质,三角形的内角和公式,中垂线的性质,解本题的关键中垂线的运用.

练习册系列答案
相关题目
18.2015年6月20日,全球迎来第十五个世界难民日,联合国难民署6月18日发布最新《全球趋势》报告,报告显示,目前全球难民总数已接近6000万,创二战以来新高,用科学记数法表示6000万为( )
| A. | 6×103 | B. | 0.6×107 | C. | 6×107 | D. | 6×108 |
19.如果等式x3•xm=x6成立,那么m=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
16.下列关于x的方程中,没有实数解的是( )
| A. | x2-4x+4=0 | B. | x2-2x-3=0 | C. | x2-2x=0 | D. | x2-2x+5=0 |
3. 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
13.一组数据,3,4,6,5,6,则这组数据的众数、中位数分别是( )
| A. | 5,6 | B. | 5,5 | C. | 6,5 | D. | 6,6 |
17. 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )
 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则AF:CF=( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
18.同一平面内,半径分别是2cm和3cm的两圆的圆心距为5cm,则这两圆的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.