题目内容
13. 如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,-2),连结OA、OD、DC、AC,四边形AODC为菱形.
如图,在平面直角坐标系xOy中,直线y=mx+1与双曲y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点D(1,-2),连结OA、OD、DC、AC,四边形AODC为菱形.(1)求k和m的值;
(2)根据图象写出反比例函数的值小于2时x的取值范围;
(3)设点P是y轴上一动点,且S△OAP=S菱形OACD,求点P的坐标.
分析 (1)由菱形的性质可知A、D关于x轴对称,可求得A点坐标,把A点坐标分别代入两函数函数解析式可求得k和m值;
(2)由(1)可知A点坐标为(1,2),结合图象可知在A点的下方时,反比例函数的值小于2,可求得x的取值范围;
(3)根据菱形的性质可求得C点坐标,可求得菱形面积,设P点坐标为(0,y),根据条件可得到关于y的方程,可求得P点坐标.
解答  解:
解:
(1)如图,连接AD,交x轴于点E,
∵D(1,2),
∴OE=1,ED=2,
∵四边形AODC是菱形,
∴AE=DE=2,EC=OE=1,
∴A(1,2),
将A(1,2)代入直线y=mx+1可得m+1=2,解得m=1,
将A(1,2)代入反比例函数y=$\frac{k}{x}$,可求得k=2;
(2)∵当x=1时,反比例函数的值为2,
∴当反比例函数图象在A点下方时,对应的函数值小于2,
此时x的取值范围为:x<0或x>1;
(3)∵OC=2OE=2,AD=2DE=4,
∴S菱形OACD=$\frac{1}{2}$OC•AD=4,
S△OAP=S菱形OACD,
∴S△OAP=4,
设P点坐标为(0,y),则OP=|y|,
∴$\frac{1}{2}$×|y|×1=4,即|y|=8,
解得y=8或y=-8,
∴P点坐标为(0,8)或(0,-8).
点评 本题为反比例函数的综合应用,涉及知识点有待定系数法、菱形的性质、三角形的面积及数形结合思想等.在(1)中求得A点的坐标是解题的关键,在(2)中注意数形结合思想的应用,在(3)中注意P点有两种情况.本题考查知识点较为基础,属于基础题,难度不大.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
3. 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
 如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )
如图,将?ABCD绕点C顺时针旋转一定角度后,得到?EFCG,若BC与CG在同一直线上,点D落在EG上,则旋转的度数为( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
4.计算$\frac{2x+y}{x-y}$-$\frac{x+2y}{x-y}$的结果是( )
| A. | 1 | B. | $\frac{x+3y}{x-y}$ | C. | x-y | D. | x+3y |
18.同一平面内,半径分别是2cm和3cm的两圆的圆心距为5cm,则这两圆的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
5.甲、乙两地之间的高速公路全长200千米,比原来国道的长度减少了20千米.高速公路通车后,某长途汽车的行驶速度提高了45千米/时,从甲地到乙地的行驶时间缩短了一半.设该长途汽车在原来国道上行驶的速度为x千米/时,根据题意,下列方程正确的是( )
| A. | $\frac{200}{x+45}$=$\frac{180}{x}$$•\frac{1}{2}$ | B. | $\frac{200}{x+45}$=$\frac{220}{x}$$•\frac{1}{2}$ | C. | $\frac{200}{x}$=$\frac{180}{x-45}$•$\frac{1}{2}$ | D. | $\frac{200}{x}$=$\frac{220}{x-45}$•$\frac{1}{2}$ |
2.4的算术平方根的相反数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | ±2 |
15.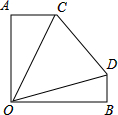 如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
 如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )| A. | 90km | B. | 50$\sqrt{2}$km | C. | 20$\sqrt{13}$km | D. | 100km |