题目内容
19. 如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.| A. | $\frac{200}{3}$ | B. | $\frac{400}{3}$ | C. | $\frac{500}{3}$ | D. | $\frac{700}{3}$ |
分析 过点D作DE⊥AB于点E,可得四边形BCDE为矩形,在Rt△ACB中,根据AB=200m,求出BC的长度,然后在Rt△ADE求出AE的长度,即可求出塔高CD.
解答 解:过点D作DE⊥AB于点E,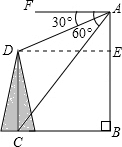
则四边形BCDE为矩形,
∵∠FAB=30°,∠FAC=60°,
∴∠CAB=30°,
在Rt△ACB中,
∵AB=200m,
∴BC=ABtan30°=$\frac{200}{3}$$\sqrt{3}$(m),
在Rt△ADE中,
∵∠DAE=60°,DE=BC=$\frac{200}{3}$$\sqrt{3}$m,
∴AE=$\frac{DE}{tan60°}$=$\frac{200}{3}$(m),
∴塔高CD=CE=200-$\frac{200}{3}$=$\frac{400}{3}$(m).
故选B.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,利用三角函数的知识求解,难度一般.

练习册系列答案
相关题目
9. 如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
 如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )| A. | 150° | B. | 240° | C. | 200° | D. | 180° |
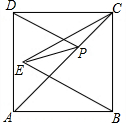
10. 如图,CD=CE,AE=BD,∠ADC=∠BEC=100°,∠ACD=26°,则∠BCD的度数是( )
如图,CD=CE,AE=BD,∠ADC=∠BEC=100°,∠ACD=26°,则∠BCD的度数是( )
 如图,CD=CE,AE=BD,∠ADC=∠BEC=100°,∠ACD=26°,则∠BCD的度数是( )
如图,CD=CE,AE=BD,∠ADC=∠BEC=100°,∠ACD=26°,则∠BCD的度数是( )| A. | 72° | B. | 54° | C. | 46° | D. | 20° |
 六一儿童节期间,某眼镜店开展优惠配镜活动,某款式的眼镜广告如图:请你为广告补上原价.
六一儿童节期间,某眼镜店开展优惠配镜活动,某款式的眼镜广告如图:请你为广告补上原价. 如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,过点P作PD∥BC,交AB于点D,点P、Q同时出发,当其中一个点停止运动时,另一个点也随之停止运动.设P、Q的运动时间为t(s)(0<t<4)
如图,在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,点P从点A出发,沿AC向点C以1cm/s的速度运动,点Q从点C出发沿CB向点B以2cm/s的速度运动,过点P作PD∥BC,交AB于点D,点P、Q同时出发,当其中一个点停止运动时,另一个点也随之停止运动.设P、Q的运动时间为t(s)(0<t<4)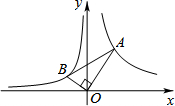 如图,已知第一象限内的点A在反比例函y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{2}$,则k的值为-1.
如图,已知第一象限内的点A在反比例函y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\frac{1}{2}$,则k的值为-1.
 如图,正方形ABCD的边长为8,△BCE是等边三角形,点E在正方形内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的边长为8,△BCE是等边三角形,点E在正方形内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )