题目内容
9. 如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )
如图,一个圆锥的母线长为6cm,底面圆的直径为8cm,则它的侧面展开扇形的圆心角度数是( )| A. | 150° | B. | 240° | C. | 200° | D. | 180° |
分析 易得圆锥的底面周长,也就是圆锥的侧面展开图的弧长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
解答 解:∵圆锥的底面半径为4cm,
∴圆锥的底面周长为8π,
设扇形的圆心角为n°,
∴$\frac{nπ×6}{180}$=8π,
解得n=240.
答:圆锥的侧面展开图中扇形的圆心角为240°.
故选B.
点评 此题主要考查了圆锥的有关计算,用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长是解题关键.

练习册系列答案
相关题目
4.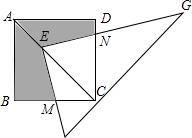 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{9}$ |
1.若点P(-m-1,-2m+6)关于y轴对称点在第二象限,则m的取值范围为( )
| A. | m>3 | B. | m<-1 | C. | -1<m<3 | D. | 不能确定 |
18.下列各式分解因式正确的是( )
| A. | $\frac{1}{2}$-2a2=$\frac{1}{2}$(1+2a)(1-2a) | B. | x2+4y2=(x+2y)2 | ||
| C. | x2-3x+9=(x-3)2 | D. | x2-y2=(x-y)2 |
19. 如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
 如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.
如图,在200米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为30°和60°,那么塔高是( )米.| A. | $\frac{200}{3}$ | B. | $\frac{400}{3}$ | C. | $\frac{500}{3}$ | D. | $\frac{700}{3}$ |
 如图,Rt△ACB,∠ACB=90°,将△ACB绕点C顺时针旋转α(0<α<180)度后,得到△DCE(点A的对应点是点D,点B的对应点是点E),连接AD,BE.若∠BED=α°,∠DAB=50°,则α的值是20°.
如图,Rt△ACB,∠ACB=90°,将△ACB绕点C顺时针旋转α(0<α<180)度后,得到△DCE(点A的对应点是点D,点B的对应点是点E),连接AD,BE.若∠BED=α°,∠DAB=50°,则α的值是20°.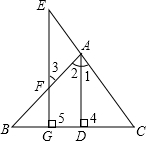 已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由. 如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,则∠D=39°,∠B=129°.
如图所示,若AB∥DC,∠1=39°,∠C和∠D互余,则∠D=39°,∠B=129°. 如图,将左方的盒子展开成为一个十字型图形,它是下图中的( )
如图,将左方的盒子展开成为一个十字型图形,它是下图中的( )


