题目内容
1.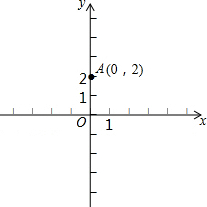 如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?
如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?
分析 根据题意画出图形,连接AP,过点A作AN⊥PM,根据线段垂直平分线的性质得出AP=PM=y,再由勾股定理即可得出结论.
解答  解:如图所示,
解:如图所示,
连接AP,过点A作AN⊥PM,
∵BP是AM的垂直平分线,
∴AP=PM=y.
∵PM⊥x轴,
∴AN=x,P(x,y),PN=y-2,
∴AN2+PN2=AP2,即x2+(y-2)2=y2,即y=$\frac{{x}^{2}}{4}$+1.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
9.一个直角三角形的直角边长分别为3和5,第三边的长是方程x2-6x+8=0的根,则这个三角形的周长为( )
| A. | 10 | B. | 12 | C. | 10或12 | D. | 以上都不对 |
12.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表
从上表可知,下列说法(1)抛物线与x轴的一个交点为(3,0);(2)抛物线y=ax2+bx+c最大值b;(3)抛物线对称轴x=$\frac{1}{2}$;(4)在对称轴左侧y随x增大而增大,正确的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.下列运算中,正确的是( )
| A. | $\sqrt{9}=±3$ | B. | (a2)3=a6 | C. | 3a•2a=6a | D. | 3-2=-6 |
 请你以直线DE为对称轴画出三角形ABC的对称图形(不写作法,要保留作图痕迹)
请你以直线DE为对称轴画出三角形ABC的对称图形(不写作法,要保留作图痕迹)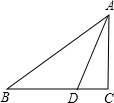 如图,△ABC中∠C=90°,点D在BC上,且DB=DA,tan∠DAC=$\frac{1}{2}$,则tanB=$\frac{\sqrt{5}-1}{2}$.
如图,△ABC中∠C=90°,点D在BC上,且DB=DA,tan∠DAC=$\frac{1}{2}$,则tanB=$\frac{\sqrt{5}-1}{2}$.