题目内容
12.下列条件:①一锐角和一边对应相等,②两边对应相等,③两锐角对应相等,其中能得到两个直角三角形全等的条件有①②(只填序号).分析 根据全等三角形的判定定理HL、AAS、AAS,SAS作出判定即可.
解答 解:①一锐角和一边对应相等可利用AAS或ASA判定两个直角三角形全等,
②两边对应相等可利用SAS或HL两个直角三角形全等,
③两锐角对应相等不能证明两个直角三角形全等,
故答案为:①②.
点评 本题考查了直角三角形全等的判定.直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它,同时,直角三角形又是特殊的三角形,有它的特殊性,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
2.若点(x1,y1)、(x2,y2)是反比例函数y=-$\frac{1}{x}$的图象上的点,并且x1<x2<0,则下列各式中正确的是( )
| A. | y1<y2 | B. | y1>y2 | C. | y1= y2 | D. | 不能确定 |
4.若一个多边形的每一个内角都相等,且一个外角等于45°,则这个多边形是( )
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
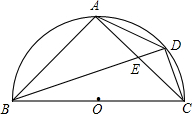 如图,BC为半圆的直径,O为圆心,D是弧AD的中点,四边形ABCD的对角线AC、BD交于点E.求证:△ABE∽△DBC.
如图,BC为半圆的直径,O为圆心,D是弧AD的中点,四边形ABCD的对角线AC、BD交于点E.求证:△ABE∽△DBC.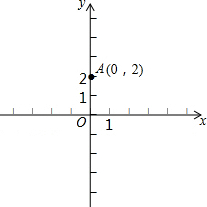 如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?
如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?