题目内容
6.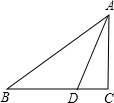 如图,△ABC中∠C=90°,点D在BC上,且DB=DA,tan∠DAC=$\frac{1}{2}$,则tanB=$\frac{\sqrt{5}-1}{2}$.
如图,△ABC中∠C=90°,点D在BC上,且DB=DA,tan∠DAC=$\frac{1}{2}$,则tanB=$\frac{\sqrt{5}-1}{2}$.
分析 在Rt△ABD中,由于tan∠DAC=$\frac{1}{2}$,设CD=k,AC=2k,根据勾股定理得到AD=$\sqrt{5}$k,求得BC=(1+$\sqrt{5}$)k,在Rt△ABC中,根据三角函数的定义即可得到结果.
解答 解:∵∠C=90°,
在Rt△ABD中,∵tan∠DAC=$\frac{1}{2}$,
∴设CD=k,AC=2k,
∴AD=$\sqrt{5}$k,
∴BD=AD=$\sqrt{5}$k,
∴BC=(1+$\sqrt{5}$)k,
在Rt△ABC中,tanB=$\frac{AC}{BC}$=$\frac{2k}{(\sqrt{5}+1)k}$=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了解直角三角形,熟练掌握直角三角形的边角关系是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.不等式组$\left\{\begin{array}{l}{\frac{1}{2}x+1>0}\\{1-x>0}\end{array}\right.$的解集( )
| A. | x>-2 | B. | x<1 | C. | -2<x<1 | D. | 无解 |
16.某小区改善生态环境,促进生活垃圾的分类处理,将少活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1000吨生活垃圾,数据统计如下(单位:吨):
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1000吨生活垃圾,数据统计如下(单位:吨):
| A | B | C | |
| m | 400 | 100 | 100 |
| n | 30 | 240 | 30 |
| p | 20 | 20 | 60 |
12.等腰三角形ABC中,AB=AC=13,BC=10,则底角B的正切值为( )
| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{5}{13}$ |
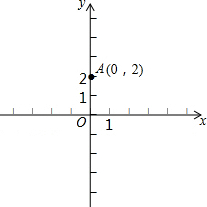 如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?
如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?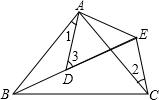 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=35°,则∠3=55°.
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=20°,∠2=35°,则∠3=55°. 观察图象,当x>4时,y>3?
观察图象,当x>4时,y>3?