题目内容
12.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用图表结合二次函数对称性,进而得出一元二次方程-x2+bx+c=0的两个根,即为y=0时x的值,即可得出判断.
解答 解:由图表可得出:x=0和1时,对应y的值为6,故x=-1和2时,对应y的值为4,
可得:(1)抛物线与x轴的一个交点为(3,0),正确;
(2)抛物线y=ax2+bx+c最大值6$\frac{1}{4}$,错误;
(3)抛物线对称轴x=$\frac{1}{2}$,正确;
(4)在对称轴左侧y随x增大而增大,正确.
故选C.
点评 此题主要考查了抛物线的性质,二次函数对称性是解题关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
4.若一个多边形的每一个内角都相等,且一个外角等于45°,则这个多边形是( )
| A. | 五边形 | B. | 六边形 | C. | 七边形 | D. | 八边形 |
16.某小区改善生态环境,促进生活垃圾的分类处理,将少活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为m,n,p,并且设置了相应的垃圾箱,“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1000吨生活垃圾,数据统计如下(单位:吨):
请根据以上信息,试估计“厨房垃圾”投放正确的概率.
(1)若将三类垃圾随机投入三类垃圾箱,请用画树状图的方法求垃圾投放正确的概率;
(2)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共1000吨生活垃圾,数据统计如下(单位:吨):
| A | B | C | |
| m | 400 | 100 | 100 |
| n | 30 | 240 | 30 |
| p | 20 | 20 | 60 |
17.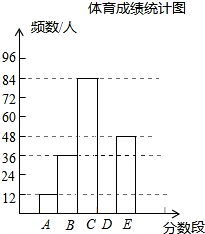 为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:
为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:
体育成绩统计表
根据上面提供的信息,回答下列问题:
(1)在统计表中,a=0.15,b=60,并将统计图补充完整;
(2)小明说:“这组数据的中位数一定在C中.”你认为小明的说法正确吗?正确(填“正确”或“错误”);
(3)若成绩在40分以上(含40分)定为优秀,则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少?
 为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:
为了了解某市初三年级学生体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:25.5~30.5;B:30.5~35.5;C:35.5~40.5;D:40.5~45.5;E:45.5~50.5)统计如下:体育成绩统计表
| 分数段 | 频数/人 | 频率 |
| A | 12 | 0.05 |
| B | 36 | a |
| C | 84 | 0.35 |
| D | b | 0.25 |
| E | 48 | 0.20 |
(1)在统计表中,a=0.15,b=60,并将统计图补充完整;
(2)小明说:“这组数据的中位数一定在C中.”你认为小明的说法正确吗?正确(填“正确”或“错误”);
(3)若成绩在40分以上(含40分)定为优秀,则该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有多少?
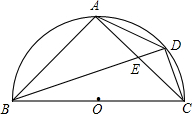 如图,BC为半圆的直径,O为圆心,D是弧AD的中点,四边形ABCD的对角线AC、BD交于点E.求证:△ABE∽△DBC.
如图,BC为半圆的直径,O为圆心,D是弧AD的中点,四边形ABCD的对角线AC、BD交于点E.求证:△ABE∽△DBC.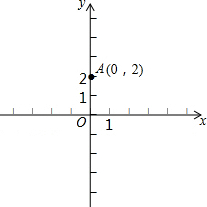 如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?
如图,在平面直角坐标系中,点A的坐标是(0,2)在x轴上任取一点M,完成以下作图步骤:连接AM,作线段AM的垂直平分线l1,过点M作x轴的垂线l2,记l1、l2的交点为P.设点P的坐标是(x,y),你能得到x,y满足的关系式吗?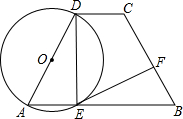 如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作
如图、在梯形ABCD中,AB∥CD,AD=BC,以AD为直径的⊙O交AB于E,过E作 已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.
已知如图:在△ABC中,AD⊥BC于D,∠B=30°,∠C=45°,BD=2$\sqrt{3}$,求AC的长.