题目内容
多项式x2+y2、-x2+y2、x2+(-y2)、8x2-y2、(y-x)2+(x-y)、2x2-
y2中,能在有理数范围内用平方差公式分解的有( )
| 1 |
| 2 |
| A、3个 | B、4个 | C、5个 | D、6个 |
考点:因式分解-运用公式法
专题:计算题
分析:原式各项利用平方差公式的结构特征判断即可.
解答:解:多项式x2+y2、-x2+y2、x2+(-y2)、8x2-y2、(y-x)2+(x-y)、2x2-
y2中,能在有理数范围内用平方差公式分解的有-x2+y2、x2+(-y2)、2x2-
y2,共3个.
故选A.
| 1 |
| 2 |
| 1 |
| 2 |
故选A.
点评:此题考查了因式分解-运用公式法,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
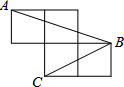 如图,每个小正方形的边长为1,则∠ABC的度数为( )
如图,每个小正方形的边长为1,则∠ABC的度数为( )| A、90° | B、60° |
| C、45° | D、30° |
两个有理数相乘,积是负数,则这两个有理数( )
| A、都是负数 | B、都是正数 |
| C、一正数一负数 | D、有一个是零 |
下列多项式不能运用平方差公式分解因式的是( )
| A、-x2-y2 |
| B、4x2-9 |
| C、x4-y4 |
| D、-a2+16 |
下列方程中,是一元二次方程的是( )
| A、x2+y2=1 | ||||
B、
| ||||
| C、4x2-5x-3=5 | ||||
D、
|
 如图,某旅游景区的湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在A处观测小岛湖岸边的P,测得P在北偏西60°的方向上,沿观光小道向西前行30米到达B处,测得P在北偏西45°的方向上,请你根据以上数据帮助小张求出小桥PD的长.(结果精确到个位,参考数据:
如图,某旅游景区的湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在A处观测小岛湖岸边的P,测得P在北偏西60°的方向上,沿观光小道向西前行30米到达B处,测得P在北偏西45°的方向上,请你根据以上数据帮助小张求出小桥PD的长.(结果精确到个位,参考数据: