题目内容
13.有一列数:第一个数为x1=1,第二个数为x2=3,第三个数开始依次记为为x3,x4,…xn;从第二个数开始,每个数是它相邻两数和的一半.(如:x2=$\frac{{x}_{1}+{x}_{3}}{2}$)(1)求第三、四、五个数,并写出计算过程;
(2)根据(1)的结果表明,推测x4=7;
(3)探索这一列数的规律,猜想第k个数xk=2k-1.(k是大于2的整数)
分析 根据题意,从第二个数开始,每个数是它相邻两数和的一半,又有第一个数x1=1,第二个数x2=3,可得第三个数为2×3-1=5,第四个数为2×4-1=7,同理第五个数为2×5-1=9;…由此可得第k个数xk=2k-1.
解答 解:(1)∵x2=$\frac{{x}_{1}+{x}_{3}}{2}$,
∴第三个数为:3×2-1=5,
第四个数为:5×2-3=7,
第五个数为:7×2-5=9,
…
∴第n个数为:2n-1;
(2)x4=2×4-1=7;
(3)xk=2k-1.
点评 此题考查数字的变化规律,通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.本题的关键规律为:xn=2n-1.

练习册系列答案
相关题目
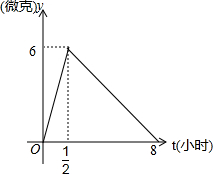 某医药研究所开发一种新药,如果承认按规定的剂量服用,据监测,服药后每毫升血液中含药量y与时间t之间关系如图所示,据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为6:00,那么服药后几点到几点有效?
某医药研究所开发一种新药,如果承认按规定的剂量服用,据监测,服药后每毫升血液中含药量y与时间t之间关系如图所示,据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为6:00,那么服药后几点到几点有效?
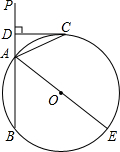 如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,
如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,