Question

2．在A、B两地之间有汽车站C，客车由A地驶往C地，货车由B经C地驶往A地，两车同时出发匀速行驶，图中客车、货车离C站路程y₁．y₂（千米）与行驶时间x（小时）之间函数关系图象，则下列说法：①A、B之间距离为280千米；②客车速度比货车每小时快30千米；③PD的解析式为y=30x-60；④E点表示两车相遇，其坐标为（$\frac{14}{3}$，80），其中正确序号为④．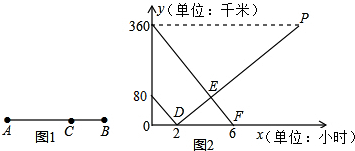

Answer 1

分析 ①根据x=0时，客车与货车距离C地的距离列式计算即可得解；
②先求出客车与货车的速度，再根据相遇问题列式求解即可；
③根据货车两小时到达C站，求得货车的速度，进一步求得到达A站的时间，进一步设直线PD解析式y与行驶时间x之间的函数关系式，列出关系式，代入点求得函数解析式即可；
④根据相遇时间求出相遇时甲行驶的路程，然后求解即可．

解答 解：x=0时，y的值为80和360，
所以，A，B两地相距80+360=440千米，故①错误；
客车的速度为：360÷6=60千米/小时，
货车的速度为：80÷2=40千米/小时，客车速度比货车每小时快20千米，故②错误；
由图可知货车的速度为80÷2=40千米/小时，
货车到达A地一共需要2+360÷40=11小时，
设PD的解析式为y=kx+b，代入点（2，0）、（11，360）得
$\left\{\begin{array}{l}{2k+b=0}\\{11k+b=360}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=40}\\{b=-80}\end{array}\right.$，
所以y=40x-80（x≥2），故③错误．
客、货两车440÷（60+40）=4.4=$\frac{14}{3}$小时相遇，故④正确．
故答案为：④．

点评 本题考查了一次函数的应用及一元一次方程的应用，解题的关键是根据题意结合图象说出其图象表示的实际意义，这样便于理解题意及正确的解题．