��Ŀ����
6�� ����ͬѧҪ֤�����⡰����Ա߷ֱ���ȵ��ı�����ƽ���ı��Ρ�����ȷ�ģ������ó߹���������ͼ��ʾ�ġ�ABCD����д���������в���������֪����֤��
����ͬѧҪ֤�����⡰����Ա߷ֱ���ȵ��ı�����ƽ���ı��Ρ�����ȷ�ģ������ó߹���������ͼ��ʾ�ġ�ABCD����д���������в���������֪����֤����֪����ͼ�����ı���ABCD�У�BC=AD��AB=CD��
��֤���ı���ABCD��ƽ���ı��Σ�
��1����ȫ��֪����֤���ڷ�������գ���
��2������ͬѧ������������ȫ�ȣ����ݡ�����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Ρ���֤�������㰴�����뷨���֤�����̣�
���� ��1����ƽ���ı��ε��ж��������ó������
��2������AC����SSS֤����ABC��CDA���ó���Ӧ����ȡ�BAC=��DCA����BCA=��DAC��֤��AB��DC��BC��AD�����ɵó����ۣ�
��� �⣺��1����ȫ��֪����֤��
��֪�����ı���ABCD�У�BC=AD��AB=CD��
��֤���ı���ABCD��ƽ���ı��Σ�
�ʴ�Ϊ��CD��ƽ�У�
��2����ͼ������AC��
�ڡ�ABC�͡�CDA�У�$\left\{\begin{array}{l}{AB=CD}&{\;}\\{BC=DA}&{\;}\\{AC=CA}&{\;}\end{array}\right.$��
���ABC��CDA��SSS����
���BAC=��DCA����BCA=��DAC��
��AB��DC��BC��AD��
���ı���ABCD��ƽ���ı��Σ�
���� ���⿼����ƽ���ı��ε��ж�������ȫ�������ε��ж�������ƽ���ߵ��ж�����������ƽ���ı��ε��ж���֤��������ȫ���ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
16���ʺ����������ġ�ABC�У�ֱ�������εĸ���Ϊ��������
��a=3��b=4��c=5��
��a=6����A=45�㣻
��a=2��b=2��c=2$\sqrt{2}$��
�ܡ�A=38�㣬��B=52�㣮
��a=3��b=4��c=5��
��a=6����A=45�㣻
��a=2��b=2��c=2$\sqrt{2}$��
�ܡ�A=38�㣬��B=52�㣮
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
14�� ��ͼ����ABC�Ķ���������������ĸ�㣬��sinA��ֵΪ��������
��ͼ����ABC�Ķ���������������ĸ�㣬��sinA��ֵΪ��������
 ��ͼ����ABC�Ķ���������������ĸ�㣬��sinA��ֵΪ��������
��ͼ����ABC�Ķ���������������ĸ�㣬��sinA��ֵΪ��������| A�� | $\frac{1}{3}$ | B�� | $\frac{\sqrt{10}}{10}$ | C�� | $\frac{\sqrt{5}}{5}$ | D�� | $\frac{3\sqrt{10}}{10}$ |

 ��������Զ������ʡ���б�ҵ������������Ŀ֮һ�������п�ǰ��ijУΪ���˽�ѧ��������Զ�ɼ�״�����Ӿ��꼶1000�������������ȡ���������μ�������Զ���ԣ���ָ���ס��ҡ�����������ͬѧ����β��Խ��������������������ͼ��������ͬѧ�ṩ�IJ�����Ϣ��
��������Զ������ʡ���б�ҵ������������Ŀ֮һ�������п�ǰ��ijУΪ���˽�ѧ��������Զ�ɼ�״�����Ӿ��꼶1000�������������ȡ���������μ�������Զ���ԣ���ָ���ס��ҡ�����������ͬѧ����β��Խ��������������������ͼ��������ͬѧ�ṩ�IJ�����Ϣ��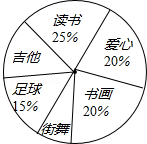 ���꼶��1�����ȫ��ͬѧ�����Լ�����Ȥ���òμ�������ѧ�����ţ�ÿ��ѧ������μ���ֻ�μ�һ������Ϊ���˽�ѧ���μ����ŵ������ѧ����Ըð�μӸ������ŵ�����������ͳ�ƣ����Ƴ�����ͼ������������ͳ��ͼ����֪�μӡ������硱��ѧ����10�ˣ������������⣺
���꼶��1�����ȫ��ͬѧ�����Լ�����Ȥ���òμ�������ѧ�����ţ�ÿ��ѧ������μ���ֻ�μ�һ������Ϊ���˽�ѧ���μ����ŵ������ѧ����Ըð�μӸ������ŵ�����������ͳ�ƣ����Ƴ�����ͼ������������ͳ��ͼ����֪�μӡ������硱��ѧ����10�ˣ������������⣺