题目内容
18.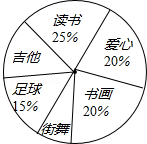 九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:
九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:(1)该班的学生共有40名;该班参加“爱心社”的人数为8名,若该班参加“吉他社”与“街舞社”的人数相同,则“吉他社”对应扇形的圆心角的度数为36°;
(2)一班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
分析 (1)利用参加“读书社”的学生数和它所占比例可计算出调查的学生总数,再用学生总数乘以“爱心社”所占的百分比得到该班参加“爱心社”的人数,然后计算出该班参加“吉他社”的百分比,用此百分比乘以360度即可得到“吉他社”对应扇形的圆心角的度数;
(3)画树状图展示所有8种等可能的结果数,再找出恰好选中甲和乙的结果数,然后根据概率公式求解.
解答 解:(1)因为参加“读书社”的学生有10人,且在扇形统计图中,所占比例为25%,
所以该班的学生共有10÷25%=40(人);
该班参加“爱心社”的人数=40×20%=8(名);
参加“吉他社”的学生在全班学生中所占比为$\frac{1}{2}$(1-25%-15%-20%-20%)=10%,
所以“吉他社”对应扇形的圆心角的度数为:360°×10%=36°;
故答案为40,8,36°;
(3)画树状图如下:
共有8种等可能的结果数,其中恰好选中甲和乙的情况有2种,
所以P(选中甲和乙)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了扇形统计图.

练习册系列答案
相关题目
8.计算(-2x2y)3,结果正确的是( )
| A. | -8x6y | B. | -6x2y3 | C. | -6x6y3 | D. | -8x6y3 |
3.某班级进行了一次诗歌朗诵比赛,甲、乙两组学生的成绩如表所示:
你认为哪一组的成绩更好一些?并说明理由.
答:乙组(填“甲”或“乙”),理由是乙组同学平均水平略高于甲组同学;且乙组同学比甲组同学成绩整齐、相对稳定.
| 组别 | 平均分 | 中位数 | 方差 |
| 甲 | 6.9 | 8 | 2.65 |
| 乙 | 7.1 | 7 | 0.38 |
答:乙组(填“甲”或“乙”),理由是乙组同学平均水平略高于甲组同学;且乙组同学比甲组同学成绩整齐、相对稳定.
 如图,直线a∥b,则∠A的度数是36°.
如图,直线a∥b,则∠A的度数是36°. 嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.
嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证. 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可)
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可) 在?ABCD中,E、F是对角线AC上两点,且AE=CF,DE=DF,四边形DEBF是菱形吗?请说明理由.
在?ABCD中,E、F是对角线AC上两点,且AE=CF,DE=DF,四边形DEBF是菱形吗?请说明理由.