题目内容
1.不等式组$\left\{\begin{array}{l}{x-3<0}\\{\frac{x-1}{2}≥-1}\end{array}\right.$的整数解为-1,0,1,2.分析 先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解即可.
解答 解:$\left\{\begin{array}{l}{x-3<0①}\\{\frac{x-1}{2}≥-1②}\end{array}\right.$,
由①得:x<3,
由②得:x≥-1,
不等式组的解集为:-1≤x<3,
则不等式组$\left\{\begin{array}{l}{x-3<0}\\{\frac{x-1}{2}≥-1}\end{array}\right.$的整数解为-1,0,1,2;
故答案为:-1,0,1,2.
点评 本题考查了不等式组的解法及整数解的确定,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列各式由左边到右边的变形,是因式分解的是( )
| A. | (a+1)(a-1)=a2-1 | B. | (x-y)(m-n)=(y-x)(n-m) | C. | ab-a-b+1=(a-1)(b-1) | D. | m2-2m-3=m(m-2)-3 |
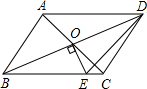 如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则?ABCD的周长为( )
如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则?ABCD的周长为( ) 如图,直线a∥b,则∠A的度数是36°.
如图,直线a∥b,则∠A的度数是36°. 嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.
嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证. 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可)
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD,请直接写出与AE相等的线段DF=FE,DF=AE(两条即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可) 在?ABCD中,E、F是对角线AC上两点,且AE=CF,DE=DF,四边形DEBF是菱形吗?请说明理由.
在?ABCD中,E、F是对角线AC上两点,且AE=CF,DE=DF,四边形DEBF是菱形吗?请说明理由.