题目内容
17.如图①,抛物线的顶点M的坐标是(1,-$\frac{27}{8}$),与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,-3).
(1)求这条抛物线的表达式;
(2)动点P从原点O出发,在线段OB上以每秒1个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒2个单位长度的速度向点C运动,当一个点到达终点时,另一个点立即停止运动,设运动时间为t秒.求t为何值时,四边形ACQP的面积有最小值,最小值是多少?
(3)如图②,当动点P运动到OB的中点时,过点P作PD⊥x轴,交抛物线于点D,连接OD,OM,MD得△ODM,将△OPD沿x轴向左平移m个单位长度(0<m<2),将平移后的三角形与△ODM重叠部分的面积记为S,求S与m的函数关系式.
分析 (1)按顶点式设出抛物线解析式,由点C在抛物线求出a即可;
(2)先求出△ABC的面积,然后用时间t表示出△QBP的面积,从而用时间t表示出四边形ACQP的面积即可;
(3)先求出D(2,-3),再表示出P1(2-m,0),D1(2-m-3,-3),E(2-m,-3+$\frac{3}{2}$m),求出直线OM解析式为y=-$\frac{27}{8}$x,最后分两种情况计算即可.
解答 解:(1)设抛物线解析式为y=a(x-1)2-$\frac{27}{8}$,
∵C(0,-3)在抛物线上,
∴a-$\frac{27}{8}$=-3,
∴a=$\frac{3}{8}$,
∴y=$\frac{3}{8}$(x-1)2-$\frac{27}{8}$=$\frac{3}{8}$x2-$\frac{3}{4}$x-3,
(2)如图1,
作QG⊥x轴,
∵y=$\frac{3}{8}$x2-$\frac{3}{4}$x-3,
∴A(-2,0),B(4,0),C(0,-3),
∴S△ABC=$\frac{1}{2}$AB×OC=$\frac{1}{2}$×6×3=9,
由运动有BP=4-t,BQ=2t,
∵QG∥OC,
∴$\frac{BQ}{BC}=\frac{QG}{OC}$,
∴$\frac{2t}{5}=\frac{QG}{3}$,
∴QG=$\frac{6t}{5}$,
∴S△QBP=$\frac{1}{2}$BP×QG=$\frac{1}{2}$×(4-t)×$\frac{6t}{5}$=-$\frac{3}{5}$(t-2)2+$\frac{12}{5}$,
∴S四边形ACQP=S△ABC-S△QBP=9-[-$\frac{3}{5}$(t-2)2+$\frac{12}{5}$]=$\frac{3}{5}$(t-2)2+$\frac{33}{5}$,
∴当t=2时,S四边形ACQP最小=$\frac{33}{5}$;
(3)如图2,
∵动点P运动到OB的中点且OB=4,
∴OP=2,
∴当x=2时,y=-3,
∴D(2,-3),
∴直线OD解析式为y=-$\frac{3}{2}$x,
∵△P1O1D1是由△POD平移得到,
∴P1(2-m,0),D1(2-m-3,-3),E(2-m,-3+$\frac{3}{2}$m)
∴直线OM解析式为y=-$\frac{27}{8}$x,
①如图2,当0<m≤$\frac{10}{9}$时,作FH⊥x轴,
∴O1(-m,0)
∵O1D1∥OD,
∴直线O1D1的解析式为y=-$\frac{3}{2}$x-$\frac{3}{2}$m,
∵$\left\{\begin{array}{l}{y=-\frac{27}{8}x}\\{y=-\frac{3}{2}x-\frac{3}{2}m}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{4}{5}m}\\{y=-\frac{27}{10}m}\end{array}\right.$,
∴F($\frac{4}{5}$m,-$\frac{27}{10}$m),
∴FH=$\frac{27}{10}$m,
∴S四边形OFD1E=S四边形OO1D1D-S△OO1F-S△DD1E=-$\frac{21}{10}$m2+3m,
②如图3,
当$\frac{10}{9}$<m<2时,设D1P1交OM于点F,
∴F(2-m,-$\frac{27}{8}$(2-m)),
∴EF=$\frac{15}{8}$(2-m),
∴S△OEF=$\frac{1}{2}$EF×OP1=$\frac{15}{16}$(2-m)2,
点评 此题是二次函数综合题,主要考查了图形面积的计算,函数极值的求法,函数解析式的确定,解本题的关键是表示线段和点的坐标.

 综合自测系列答案
综合自测系列答案| A. | -8x6y | B. | -6x2y3 | C. | -6x6y3 | D. | -8x6y3 |
 经过调查研究显示:机动车尾气是某城市PM2.5的最大来源,一辆车每行驶20千米平均向大气里排放0.035千克污染物,某校环保志愿小分队从环保局了解到此城市100天的空气质量等级情况.并制成统计图和表:
经过调查研究显示:机动车尾气是某城市PM2.5的最大来源,一辆车每行驶20千米平均向大气里排放0.035千克污染物,某校环保志愿小分队从环保局了解到此城市100天的空气质量等级情况.并制成统计图和表:| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 10 | a | 12 | 8 | 25 | b |
(2)小明是社区环保志愿者,他和同学们调查了机动车每天的行驶路程,了解到每辆车每天平均出行25千米.已知该市2015年机动车保有量已突破200万辆,请你通过计算,估计2015年该市一天中出行的机动车至少要向大气里排放多少千克污染物?
 如图所示的中国象棋棋盘上,若“帅”位于点(0,-2)上,“相”位于点(2,-2)上,则“炮”位于点( )
如图所示的中国象棋棋盘上,若“帅”位于点(0,-2)上,“相”位于点(2,-2)上,则“炮”位于点( )| A. | (-3,2) | B. | (-3,1) | C. | (-2,1) | D. | (-2,2) |
 如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=$\frac{{\sqrt{3}}}{2}$,线段AD、AB的长分别是方程x2-11x+24=0的两根(AD>AB).
如图,矩形ABCD的顶点A在x轴的正半轴上,顶点D在y轴的正半轴上,点B、点C在第一象限,sin∠OAD=$\frac{{\sqrt{3}}}{2}$,线段AD、AB的长分别是方程x2-11x+24=0的两根(AD>AB).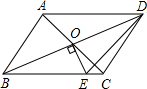 如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则?ABCD的周长为( )
如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则?ABCD的周长为( ) 如图,直线a∥b,则∠A的度数是36°.
如图,直线a∥b,则∠A的度数是36°. 嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.
嘉琪同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的□ABCD,并写出了如下尚不完整的已知和求证.