题目内容
10.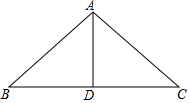 如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)
如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)
分析 根据等腰三角形的三线合一,可知AD⊥BC,根据AD=$\sqrt{A{B^2}-B{D^2}}$计算即可.
解答 解:∵AB=AC=4m,AD是△ABC的中线,BC=6m,
∴AD⊥BC,BD=$\frac{1}{2}$BC=3m,
由勾股定理,得AD=$\sqrt{A{B^2}-B{D^2}}$=$\sqrt{{4^2}-{3^2}}$=$\sqrt{7}$(m),
即这根中柱AD的长度是$\sqrt{7}$m.
点评 本题考查勾股定理的应用,等腰三角形的性质等知识,解题的关键是灵活运用所学知识,属于中考常考题型.

练习册系列答案
相关题目
19.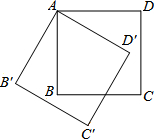 如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
 如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )
如图,将边长为4cm的正方形ABCD绕点S顺时针旋转到四边形AB′C′D′的位置,旋转角为30°,则C点运动到C′点的路径长为( )| A. | $\frac{2}{3}$πcm | B. | $\frac{2\sqrt{2}}{3}$πm | C. | $\frac{2\sqrt{3}}{3}$cm | D. | $\frac{2\sqrt{5}}{3}$cm |
20.若双曲线y=$\frac{1-k}{x}$的图象在第一、三象限,则k的取值范围为( )
| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
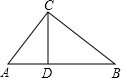 红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m.如果沿CD修一条水渠且D点在边AB上,水渠的造价为10元/m,问D点在什么位置时,水渠的造价最低?最低造价是多少?
 如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,如果BC=2AD,那么S△ADC:S△ABC的值为1:2.
如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,如果BC=2AD,那么S△ADC:S△ABC的值为1:2. 如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F.
如图,矩形ABCD中,AB=$\sqrt{3}$,BC=$\sqrt{6}$,点E在对角线BD上,且BE=1.8,连接AE并延长交DC于点F.