题目内容
1.(1)如图①,BD、CD是∠ABC和∠ACB的角平分线且交于点D,请猜想∠A与∠D之间的数量关系,并说明理由;(2)如图②,BC、CD是∠ABC和∠ACB外角的平分线且相交于点D,请猜想∠A与∠D之间的数量关系,不用说明理由;
(3)如图③,BD为∠ABC的角平分线,CD为∠ACB的外角的角平分线,它们相交于点D,请猜想∠A与∠D之间的数量关系,并说明理由
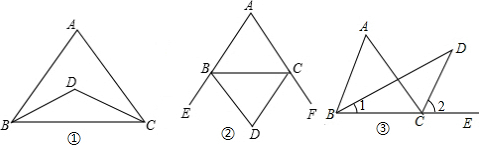
分析 (1)根据角平分线的定义得到∠DBC=$\frac{1}{2}$∠ABC,∠DCB=$\frac{1}{2}$∠ACB,根据三角形内角和定理和计算即可;
(2)根据角平分线的定义得到∠DBC=$\frac{1}{2}$∠EBC,∠FCB=$\frac{1}{2}$∠ACB,根据三角形内角和定理和计算即可;
(3)根据角平分线的定义得到∠DBC=$\frac{1}{2}$∠ABC,∠DCE=$\frac{1}{2}$∠ACE,根据三角形的外角的性质解答.
解答 解:(1)∵BD、CD是∠ABC和∠ACB的角平分线,
∴∠DBC=$\frac{1}{2}$∠ABC,∠DCB=$\frac{1}{2}$∠ACB,
∴∠D=180°-(∠DBC+∠DCB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A;
(2)BC、CD是∠ABC和∠ACB外角的平分线,
∴∠DBC=$\frac{1}{2}$∠EBC,∠FCB=$\frac{1}{2}$∠ACB,
∴∠D=180°-(∠DBC+∠DCB)=180°-$\frac{1}{2}$(∠EBC+∠FCB)=180°-$\frac{1}{2}$(180°+∠A)=90°-$\frac{1}{2}$∠A;
(3)∵BD为∠ABC的角平分线,CD为∠ACB的外角的角平分线,
∴∠DBC=$\frac{1}{2}$∠ABC,∠DCE=$\frac{1}{2}$∠ACE,
∠D=∠2-∠1=$\frac{1}{2}$(∠ACE-∠ABC)=$\frac{1}{2}$∠A.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
| A. | 5 | B. | 8 | C. | 16 | D. | 5或16 |
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
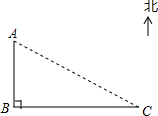 如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?
如图,在海上观察所A处.我边防海警发现正南方向60海里的B处有一可疑船只正以每小时20海里的速度向正东方向C处驶去,我边防海警即刻从A处派快艇去拦截.若快艇的速度是每小时$\frac{100}{3}$海里.问快艇最快几小时拦截住可疑船只?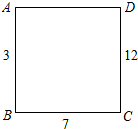 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的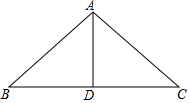 如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)
如图,木工师傅做一个“人”字形屋梁,上弦AB=AC=4m,跨度BC为6m.现有一根木料打算做中柱AD (AD是△ABC的中线),请你通过计算求出中柱AD的长度.(只考虑长度,不计损耗)