题目内容
19.一根长为1.5米的圆柱体木材,锯掉4分米长的一段后,表面积减少了50.24平方分米,这根木料原来的体积是多少立方米?分析 设圆柱体木材的底面半径为r,根据表面积减少的表面积即为锯掉4分米长的侧面积,求出r的值,即可确定出原来的体积.
解答 解:设圆柱体木材的底面半径为r,
根据题意得:2πrl=50.24,即2πr•0.4=50.24,
解得:r=$\frac{6.55}{π}$,
则这根木料原来的体积是πr2•h=π×$\frac{6.5{5}^{2}}{{π}^{2}}$×1.5=$\frac{64.35375}{π}$立方米.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.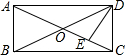 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )| A. | 36° | B. | 9° | C. | 27° | D. | 18° |
11. 如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
 如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )| A. | 10cm | B. | 11cm | C. | 12cm | D. | 13cm |
 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和. 如图,将△ABC绕着点C按顺时针方向旋转15°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是75°.
如图,将△ABC绕着点C按顺时针方向旋转15°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是75°.