题目内容
2.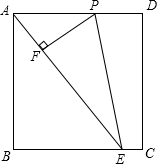 如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.
如图,矩形ABCD中,AB=4,E是BC边上一点,且BE=3,点P是射线AD上的一个动点,过点P作PF⊥AE,垂足为F,连接PE.(1)△PFA与△ABE相似吗?请说明理由;
(2)若△PFE与△ABE相似,求PA的长.
分析 (1)由四边形ABCD是矩形,得到∠B=90°,AD∥BC,根据平行线的性质得到∠PAF=∠AEB,于是得到△PFA∽△ABE;
(2)在Rt△ABEz中,根据勾股定理得到AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5,设AP=x,由(1)证得△PFA∽△ABE,根据比例式$\frac{AP}{AE}=\frac{AF}{BE}$,得到AF=$\frac{3}{5}$x,EF=5-$\frac{3}{5}$x,PF=$\sqrt{A{P}^{2}-A{F}^{2}}$=$\frac{4}{5}$x,由于△PFE与△ABE相似,于是得到$\frac{PF}{BE}=\frac{EF}{AB}$,或$\frac{PF}{AB}=\frac{EF}{BE}$,代入数值即可求得结果.
解答 解:(1)相似,
理由:∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠PAF=∠AEB,
∵PF⊥AE,
∴∠AFP=90°=∠B,
∴△PFA∽△ABE;
(2)在Rt△ABEz中,
∵AB=4,BE=3,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=5,
设AP=x,
由(1)证得△PFA∽△ABE,
∴$\frac{AP}{AE}=\frac{AF}{BE}$,
∴AF=$\frac{3}{5}$x,
∴EF=5-$\frac{3}{5}$x,PF=$\sqrt{A{P}^{2}-A{F}^{2}}$=$\frac{4}{5}$x,
∵△PFE与△ABE相似,
∴$\frac{PF}{BE}=\frac{EF}{AB}$,或$\frac{PF}{AB}=\frac{EF}{BE}$,
即$\frac{\frac{4}{5}x}{3}=\frac{5-\frac{3}{5}x}{4}$,或$\frac{\frac{4}{5}x}{4}=\frac{5-\frac{3}{5}x}{3}$,
解得:x=3,或x=$\frac{25}{6}$,
∴AP=3,或AP=$\frac{25}{6}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,矩形的性质,特别是(2)要分类讨论.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案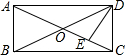 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )| A. | 36° | B. | 9° | C. | 27° | D. | 18° |
 如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )
如图,已知点A、B、C、D在同一直线上,△AEC≌△DFB,如果AD=37cm,BC=15cm,那么AB的长为( )| A. | 10cm | B. | 11cm | C. | 12cm | D. | 13cm |
 如图,在?ABCD中,已知AB=4cm,BC=9cm,∠B=30°,求?ABCD的面积.
如图,在?ABCD中,已知AB=4cm,BC=9cm,∠B=30°,求?ABCD的面积. 如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和.
如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的和.