题目内容
9.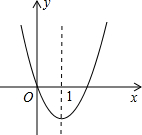 二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.
二次函数y=x2+bx的图象如图所示,对称轴为直线x=1.(1)求b的值;
(2)若直线l∥x轴,且与二次函数y=x2+bx的图象有两个公共点A,B,当点A的横坐标为-2时,求点B的坐标;
(3)若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,直接写出t的取值范围.
分析 (1)根据二次函数的对称轴列方程求解即可得到b的值;
(2)根据二次函数的对称性求出点B的横坐标,然后代入函数解析式求出纵坐标,即可得解;
(3)根据二次函数解析式求出最小值,再求出x=4时的函数值,然后根据二次函数的增减性写出t的取值范围即可.
解答 解:(1)∵对称轴为直线x=1,
∴-$\frac{b}{2}$=1,
解得b=-2;
(2)∵点A的横坐标为-2时,对称轴为直线x=1,
∴点B的横坐标为2×1-(-2)=4,
∴点B的纵坐标为42-2×4=8,
∴点B的坐标为(4,8);
(3)当x=1时,y=12-2×1=-1,
所以,在-1<x<4的范围内,-1≤y<8,
x2+bx-t=0可变形为x2+bx=t,
所以,-1≤t<8.
点评 本题考查了二次函数的性质,主要利用了二次函数的对称轴,二次函数的增减性以及最值问题,(2)利用对称性求出点B的横坐标更简便,(3)要注意自变量的取值范围的影响.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.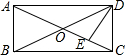 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
 如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )
如图,矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为( )| A. | 36° | B. | 9° | C. | 27° | D. | 18° |
1.已知点P是矩形ABCD内一点,连结AP、BP、CP、DP,若S△ABP+S△CDP=S△ADP+S△BCP,则关于点P的位置,正确的说法是( )
| A. | 一定是对角线交点 | B. | 一定在对角线上 | ||
| C. | 一定在对边中点的连线上 | D. | 可以是任意位置 |
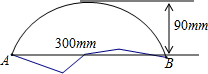 一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?
一支考古队发现一个残破的古代圆盘碎片,如图所示,考古家测量了弦AB=300mm,圆弧的高为90mm,于是得到了古圆盘的半径,从而确定了它的圆心,终于使这个古物得以复原,请问你知道考古家怎样得到它的半径吗?