题目内容
16．
如图，在平行四边形ABCD中，E为AD上一点，∠EBC=40°，且BE=BC，CE=CD，则∠A=110°．
分析 先根据平行四边形的性质得出∠2=∠3，再根据BE=BC，CE=CD，∠1=∠2，∠3=∠D，进而得出∠1=∠2=∠3=∠D，求出∠D=70°，即可得出∠A的度数．
解答 解：如图所示：
∵四边形ABCD是平行四边形，
∴AD∥BC，CD=AB，AB∥CD，
∴∠2=∠3，∠A+∠D=180°，
∵BE=BC，CE=CD，
∴BE=BC=10，CE=CD=6，∠1=∠2，∠3=∠D，
∴∠1=∠2=∠3=∠D，
∵∠EBC=40°，
∴∠D=∠1=∠3=70°，
∴∠A=180°-70°=110°；
故答案为：110°．
点评 本题考查了等腰三角形的性质及平行四边形的性质，根据题意得出∠1=∠2=∠3=∠D是解答此题的关键．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
4．
如图，有一块直角三角形纸片，两直角边分别为：AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
如图，有一块直角三角形纸片，两直角边分别为：AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）| A． | 2 cm | B． | 3 cm | C． | 4 cm | D． | 5 cm |
11．下列计算中，正确的是（ ）
| A． | （xn）3n=x4n | B． | （x2）3+（x3）2=2x6 | C． | （a3）n+1=a3n+1 | D． | （-a2）4•a8=-a16 |
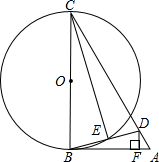如图，在△ABC中，D为AC上一点，且CD=CB，以BC为直径作⊙O，交BD于点E，连接CE，过D作DF⊥AB于点F，∠BCD=2∠ABD．
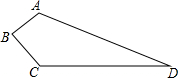某小区有一块四边形空地（如图所示，四边形ABCD），规划在这块空地上种植毎平方米60元的草坪用以美化环境，施工人员测得（单位：米）：AB=3，BC=4，CD=12，DA=13，∠B=90°，求小区种植这种草坪需多少钱？
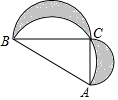如图，Rt△ABC中，∠C=90°，AC=4，BC=9，分别以它的三边为直径向上作三个半圆，则图中阴影部分面积为18-$\frac{47}{8}$π．