题目内容
16.已知,直线l1:y=3x-2k与直线l2:y=x+k交点P的纵坐标为5,直线l1与直线l2与y轴分别交于A、B两点.(1)求出P的横坐标及k的值;
(2)求△PAB的面积.
分析 (1)先将y=3x-2k代入y=x+k,求出x=$\frac{3}{2}$k,y=$\frac{5}{2}$k,由点P的纵坐标为5,得出$\frac{5}{2}$k=5,解得k=2,进而得到P的横坐标为3;
(2)先求出A、B两点坐标,再根据三角形的面积公式求出△PAB的面积.
解答 解:(1)将y=3x-2k代入y=x+k,
得3x-2k=x+k,得x=$\frac{3}{2}$k,
将x=$\frac{3}{2}$k代入y=x+k,得y=$\frac{5}{2}$k,
则点P的坐标为($\frac{3}{2}$k,$\frac{5}{2}$k).
∵点P的纵坐标为5,
∴$\frac{5}{2}$k=5,
解得k=2,
∴$\frac{3}{2}$k=3,
∴P的横坐标为3;
(2)∵直线l1:y=3x-4,
∴A点坐标为(0,-4).
∵直线l2:y=x+2,
∴B点坐标为(0,2),
∴△PAB的面积=$\frac{1}{2}$×6×3=9.
点评 本题考查了两条直线的交点问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.也考查了三角形的面积.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
7.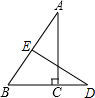 如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
 如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
4.在△ABC中,AC=6,BC=8,AB=10,则点C到AB边的距离是( )
| A. | $\frac{24}{5}$ | B. | $\frac{5}{24}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
8.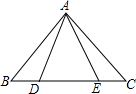 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )| A. | △ABD和△ACE成轴对称 | B. | △ABD和△ACE成中心对称 | ||
| C. | △ABD经过旋转可以和△ACE重合 | D. | △ABD经过平移可以和△ACE重合 |
5.礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A. | m+n | B. | mn+1 | C. | m+(n-1) | D. | n+(n+1) |
 如图,AD是△ABC中∠BAC的平分线,DE⊥AB于E,若S△ABC=10,DE=3cm,AB=4cm,则AC的长为$\frac{8}{3}$cm.
如图,AD是△ABC中∠BAC的平分线,DE⊥AB于E,若S△ABC=10,DE=3cm,AB=4cm,则AC的长为$\frac{8}{3}$cm.