题目内容
4.在△ABC中,AC=6,BC=8,AB=10,则点C到AB边的距离是( )| A. | $\frac{24}{5}$ | B. | $\frac{5}{24}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
分析 首先利用勾股定理逆定理证明△ABC是直角三角形,再过C点作AB的垂线,垂足为D,由“面积法”可知$\frac{1}{2}$CD×AB=$\frac{1}{2}$AC×BC,代入数据进行计算即可.
解答  解:∵62+82=102,
解:∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
过C点作DC的垂线,垂足为D,由“面积法”可知,
$\frac{1}{2}$CD×AB=$\frac{1}{2}$AC×BC,
即BD×10=8×6,
∴BD=$\frac{24}{5}$,
即点B到AC的距离是$\frac{24}{5}$,
故选:A.
点评 此题主要考查了勾股定理逆定理,以及三角形的面积,关键是理解点C到AB的距离是从点C向AB作垂线交AB于点D,即线段CD的长度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )
如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )
如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )| A. | 45° | B. | 30° | C. | 25° | D. | 20° |
14.已知一元二次方程2x2+x+k=0无实数根,那么反比例函数y=$\frac{k}{x}$的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 无法确定 |
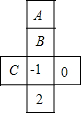 如图所示,这是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们在折成正方形后相对的面上的两个数互为相反数,则A+B+C的值是-1.
如图所示,这是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们在折成正方形后相对的面上的两个数互为相反数,则A+B+C的值是-1.