题目内容
7.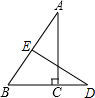 如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
分析 根据直角三角形的性质得到AB=6cm,证明△ACB≌△DEB,求出BD=6cm,计算即可.
解答 解:∵∠ACB=90°,∠BAC=30°,BC=3cm,
∴AB=2BC=6cm,
∵DE是AB的垂直平分线,
∴BE=3cm,
在△ACB和△DEB中,
$\left\{\begin{array}{l}{∠B=∠B}\\{BC=BE}\\{∠ACB=∠DEB}\end{array}\right.$,
∴△ACB≌△DEB,
∴BD=AB=6cm,又BC=3cm,
∴CD=3cm,
故选:B.
点评 本题考查的是线段垂直平分线的性质和直角三角形的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等、在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
17.如果弧长为6π的弧所对的圆心角为60°,那么这条弧所在的圆的半径是( )
| A. | 18 | B. | 12 | C. | 36 | D. | 6 |
18.下列计算错误的是( )
| A. | 1.9°=6840″ | B. | 90′=1.5° | C. | 32.15°=32°15′ | D. | 2700″=45′ |
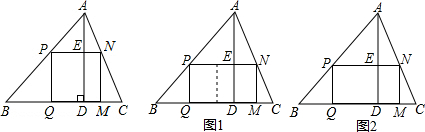
 如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)
如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)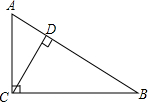 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD=$\frac{36}{5}$.