题目内容
2.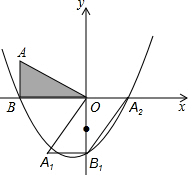 如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.(1)求抛物线的解析式.
(2)在第四象限内,抛物线上的点P在什么位置时,△PA2B1的面积最大?求出这时点P的坐标.
(3)在第四象限内,抛物线上是否存在点Q,使点Q到线段A2B1的距离为$\frac{1}{4}$?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (1)首先根据旋转的性质确定点B、B1、A2三点的坐标,然后利用待定系数法求得抛物线的解析式;
(2)求出△PA2B1的面积表达式,这是一个关于P点横坐标的二次函数,利用二次函数求极值的方法求出△PA2B1面积的最大值;值得注意的是求△A2B1面积的方法;
(3)本问引用了(2)问中三角形面积表达式的结论,利用解一元二次方程求得Q点的坐标.
解答 解:(1)∵AB⊥x轴,AB=3,tan∠AOB=$\frac{3}{4}$,
∴OB=4,
∴B(-4,0),B1(0,-4),A2(3,0).
∵抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2,
∴$\left\{\begin{array}{l}{16a-4b+c=0}\\{c=-4}\\{9a+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{1}{3}}\\{c=-4}\end{array}\right.$.
∴抛物线的解析式为:y=$\frac{1}{3}$x2+$\frac{1}{3}$x-4.
(2)设点P(m,$\frac{1}{3}$m2+$\frac{1}{3}$m-4)是第四象限内抛物线y=$\frac{1}{3}$x2+$\frac{1}{3}$x-4上的一点,$S=\frac{3}{2}(-\frac{1}{3}{m^2}-\frac{1}{3}m+4)+2m-6=-\frac{1}{2}{m^2}+\frac{3}{2}m$,
当$m=\frac{3}{2}$时,△PA2B1的面积最大,$\frac{1}{3}{m^2}+\frac{1}{3}m-4=-\frac{11}{4}$,
即点P($\frac{3}{2},-\frac{11}{4}$);
(3)假设在第四象限的抛物线上存在点Q(n,$\frac{1}{3}$n2+$\frac{1}{3}$n-4),使点Q到A2B1的距离为$\frac{1}{4}$,
则$-\frac{1}{2}{n^2}+\frac{3}{2}n=\frac{5}{8}$,
解得${n_1}=\frac{5}{2},{n_2}=\frac{1}{2}$.
因此,点Q的坐标是($(\frac{5}{2},-\frac{13}{12})$)或($(\frac{1}{2},-\frac{15}{4})$).
点评 本题综合考查了待定系数法求抛物线解析式、二次函数图象上点的坐标特征、一元二次方程、旋转与坐标变化、图形面积求法、勾股定理等重要知识点.第(2)问起承上启下的作用,是本题的难点与核心,其中的要点是坐标平面内图形面积的求解方法,这种方法是压轴题中常见的一种解题方法,同学们需要认真掌握.

 阅读快车系列答案
阅读快车系列答案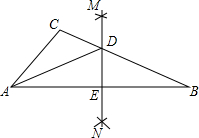 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}AB$长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}AB$长为半径画弧,两弧相交于点M、N,连接MN,交BC于点D,交AB于点E,连接AD.若△ABC的周长等于16,△ADC的周长为9,那么线段AE的长等于( )| A. | 3 | B. | 3.5 | C. | 5 | D. | 7 |
 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )| A. | 1:2 | B. | 1:4 | C. | 1:3 | D. | 4:1 |

 给一个圆锥形零件的侧面涂漆,零件的尺寸要求如图所示,求需要涂漆的面积(保留π).
给一个圆锥形零件的侧面涂漆,零件的尺寸要求如图所示,求需要涂漆的面积(保留π). (1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度;
(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M、N分别是AC、BC的中点,求线段MN的长度; 已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).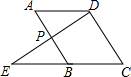 如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于E点,求证:BE=AD.
如图,平行四边形ABCD中,点P是AB的中点,延长DP交CB的延长线于E点,求证:BE=AD.