题目内容
12. 如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )
如图,已知△ADE与△ABC的相似比为1:2,则△ADE与四边形DBCE的面积比为( )| A. | 1:2 | B. | 1:4 | C. | 1:3 | D. | 4:1 |
分析 根据相似三角形面积的比等于相似比的平方,求出△ADE与△ABC的面积比,计算得到答案.
解答 解:∵△ADE与△ABC的相似比为1:2,
∴△ADE与△ABC的面积比为1:4,
∴△ADE与四边形DBCE的面积比为1:3,
故选:C.
点评 本题考查的是相似三角形的性质,掌握相似三角形面积的比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
3.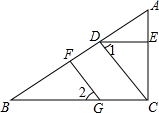 如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
(1)FG∥DC;(2)∠AED=∠ACB;(3)CD平分∠ACB;(4)∠1+∠B=90°;(5)∠BFG=∠BDC.
 如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )
如图,如果∠1=∠2,DE∥BC,则下列结论正确的个数为( )(1)FG∥DC;(2)∠AED=∠ACB;(3)CD平分∠ACB;(4)∠1+∠B=90°;(5)∠BFG=∠BDC.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7. 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
17.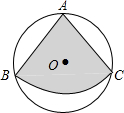 如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
 如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )
如图,从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为( )| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
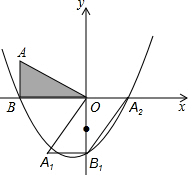 如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.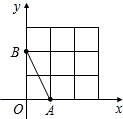 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上. 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且DE=6cm,则CD=6cm.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且DE=6cm,则CD=6cm. 某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为4米,tanα=1.6,tanβ=1.2,试求建筑物CD的高度.
某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为α.测得A,B之间的距离为4米,tanα=1.6,tanβ=1.2,试求建筑物CD的高度.