题目内容
17. 已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).
已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).(1)求m的值;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,并写出该函数在-3<x≤-$\frac{2}{3}$时对应的函数值y的取值范围;
(3)设一次函数y2=nx+3(n≠0),问是否存在正整数n使得(2)中函数的函数值y=y2时,对应的x的值为-1<x<0?若存在,求出n的值;若不存在,说明理由.
分析 (1)根据抛物线y1=x2+4x+1的图象向上平移m个单位,可得y2=x2+4x+1+m,再利用点(1,8)在图象上,求出m即可;
(2)根据函数解析式画出图象,即可得出函数大小分界点;
(3)根据当y=y3且对应的-1<x<0时,x2+4x+3=nx+3,得出n取值范围即可得出答案.
解答  解:(1)由题意可得y2=x2+4x+1+m,
解:(1)由题意可得y2=x2+4x+1+m,
又∵点(1,8)在图象上,
∴8=1+4×1+1+m,
∴m=2;
(2)如图所示:由(1)得平移后抛物线解析式为:y=x2+4x+3,
则在x轴下方的部分沿x轴翻折到x轴上方的抛物线解析式为:y=-x2-4x-3,
故y=$\left\{\begin{array}{l}{{x}^{2}+4x+3(x≤-3或x≥-1)}\\{-{x}^{2}-4x-3(-3<x<-1)}\end{array}\right.$,
当-3<x≤-$\frac{2}{3}$时,0<y≤$\frac{7}{9}$;
(3)不存在,
理由:当y=y3且对应的-1<x<0时,x2+4x+3=nx+3,
∴x1=0,x2=n-4,
且-1<n-4<0得3<n<4,
∴不存在正整数n满足条件.
点评 此题主要考查了二次函数的综合应用以及图象交点求法,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.

练习册系列答案
相关题目
7. 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
 实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )
实数a,b在数轴上的位置如图所示,若a=-3,则b等于( )| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
 如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形.
如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形. 一个包装盒的表面展开图如图所示,包装盒的容积为750cm3,请写出关于x的方程15x(30-2x)÷2=750,化成一般形式是x2-15x+50=0.
一个包装盒的表面展开图如图所示,包装盒的容积为750cm3,请写出关于x的方程15x(30-2x)÷2=750,化成一般形式是x2-15x+50=0.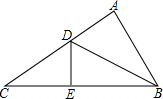 如图,在△BAC中,AB=3,BC=5,AC=4,现将它折叠,使点C与点B重合,DE为折痕,求CD的长.
如图,在△BAC中,AB=3,BC=5,AC=4,现将它折叠,使点C与点B重合,DE为折痕,求CD的长.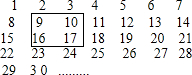 把连续的正整数1,2,3,4,…,按如图方式列成一个数表.
把连续的正整数1,2,3,4,…,按如图方式列成一个数表.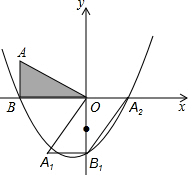 如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
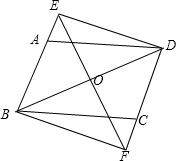
如图,AB⊥x轴于点B,AB=3,tan∠AOB=$\frac{3}{4}$,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2. 如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.
如图是凹四边形ABCD,已知AB=4,BC=3,∠ABC=90°,且CD=13,DA=12,这个凹四边形的面积等于24.