题目内容
9.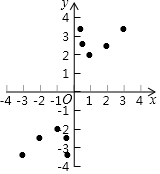 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:(1)自变量x的取值范围是x≠0;
(2)如表是y与x的几组对应数值:
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
(3)进一步探究发现:该函数在第一象限内的最低点的坐标是(1,2),观察函数图象,写出该函数的另一条性质x>1时,y随x增大而增大;0<x<1时,y随x增大而减小;
(4)请你利用配方法证明:当x>0时,y=x+$\frac{1}{x}$的最小值为2.(提示:当x>0时x=($\sqrt{x}$)2,$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2)
分析 (1)由分母不能为零,即可得出自变量x的取值范围;
(2)描点、连线,画出函数图象即可;
(3)观察函数图象,找出该函数的另一条性质即可;
(4)由x=($\sqrt{x}$)2、$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2、$\sqrt{x}$•$\frac{1}{\sqrt{x}}$=1,利用配方法即可得出x+$\frac{1}{x}$=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2+2≥2,由此即可得出:当x>0时,y=x+$\frac{1}{x}$的最小值为2.
解答 解:(1)∵x在分母上,
∴自变量x的取值范围是x≠0.
故答案为:x≠0.
(2)画出函数图象,如图所示.
(3)x>1时,y随x增大而增大;0<x<1时,y随x增大而减小.
故答案为:x>1时,y随x增大而增大;0<x<1时,y随x增大而减小.
(4)∵当x>0时,x=($\sqrt{x}$)2,$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2,且$\sqrt{x}$•$\frac{1}{\sqrt{x}}$=1,
∴x+$\frac{1}{x}$=($\sqrt{x}$)2+($\frac{1}{\sqrt{x}}$)2=($\sqrt{x}$)2-2+($\frac{1}{\sqrt{x}}$)2+2=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2+2,
∵($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2≥0,
∴($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2+2≥2,
∴x+$\frac{1}{x}$≥2,即当x>0时,y=x+$\frac{1}{x}$的最小值为2.
点评 本题考查了反比例函数的性质、配方法的应用以及反比例函数的图象,解题的关键是:(1)由分母不能为零,找出自变量x的取值范围;(2)描点.连线,画出函数图象;(3)观察函数图象,找出函数的性质;(4)利用配方法找出x+$\frac{1}{x}$=($\sqrt{x}$-$\frac{1}{\sqrt{x}}$)2+2≥2.

 阅读快车系列答案
阅读快车系列答案| A. | 第一次向左拐40°,第二次向右拐40° | |
| B. | 第一次向右拐50°,第二次向左拐130° | |
| C. | 第一次向右拐60°,第二次向右拐120° | |
| D. | 第一次向左拐110°,第二次向右拐110° |
 如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )
如图,在平面直角坐标系中xOy中,已知点A(0,1),以OA为边在右侧作等边三角形OAA1,再过点A1作x轴的垂线,垂足为点O1,以O1A1为边在右侧作等边三角形O1A1A2;…按此规律继续作下去,得到等边三角形O2016A2016A2017,则点A2017的纵坐标为( )| A. | ($\frac{1}{2}$)2017 | B. | ($\frac{1}{2}$)2016 | C. | ($\frac{1}{2}$)2015 | D. | ($\frac{1}{2}$)2014 |
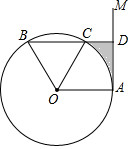 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.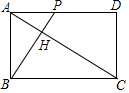 如图,已知矩形ABCD中,AB=2,AD=2$\sqrt{3}$,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①点H不可能在矩形ABCD之外;②AH的最小值为$\sqrt{7}$-$\sqrt{3}$;③在运动过程中,BP扫过的面积始终等于CH扫过的面积;④在运动过程中,点H的运动路线(轨迹)长为$\frac{2}{3}$$\sqrt{3}$π,正确的有(填序号)①②④.
如图,已知矩形ABCD中,AB=2,AD=2$\sqrt{3}$,动点P从点A出发向终点D运动,连BP,并过点C作CH⊥BP,垂足为H.①点H不可能在矩形ABCD之外;②AH的最小值为$\sqrt{7}$-$\sqrt{3}$;③在运动过程中,BP扫过的面积始终等于CH扫过的面积;④在运动过程中,点H的运动路线(轨迹)长为$\frac{2}{3}$$\sqrt{3}$π,正确的有(填序号)①②④.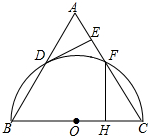 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E. 如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.
如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°. 己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.
己知A(-1,0),B(2,0),点P是直线y=x+4上的一动点且在x轴上方,如果以点A、B、P、Q为顶点的平行四边形的面积等于6,画出图形并求出点P和点Q的坐标.