题目内容
14.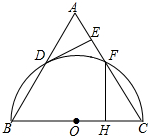 如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若AB=4,则弦FC和弧FC组成的弓形面积$\frac{2}{3}$π-$\sqrt{3}$.
分析 (1)连接OD,由等边三角形的性质得出AB=BC,∠B=∠C=60°,证出△OBD是等边三角形,得出∠BOD=∠C,证出OD∥AC,得出DE⊥OD,即可得出结论;
(2)先证明△OCF是等边三角形,得出CF=OC=$\frac{1}{2}$BC=$\frac{1}{2}$AB=2,再由三角函数即可求出FH,然后根据扇形和三角形的面积公式即可得到结论.
解答 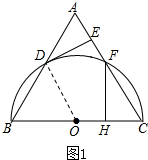 解:(1)DE是⊙O的切线;理由如下:
解:(1)DE是⊙O的切线;理由如下:
连接OD,如图1所示:
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠C=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴∠BOD=60°,
∴∠BOD=∠C,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)连接OF,如图2所示: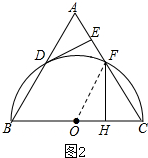
∵OC=OF,∠C=60°,
∴△OCF是等边三角形,
∴∠COF=60°,
CF=OC=$\frac{1}{2}$BC=$\frac{1}{2}$AB=2,
∵FH⊥BC,
∴∠FHC=90°,
∴FH=CF•sin∠C=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴弦FC和弧FC组成的弓形面积=S扇形COF-S△COF=$\frac{60•π×{2}^{2}}{360}$-$\frac{1}{2}$×2×$\sqrt{3}$=$\frac{2}{3}$π-$\sqrt{3}$,
故答案为:$\frac{2}{3}$π-$\sqrt{3}$.
点评 本题考查了切线的判定、等边三角形的性质与判定、平行线的判定、三角函数;熟练掌握等边三角形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )| A. | 1.8 | B. | 2.4 | C. | 3.2 | D. | 3.6 |
9.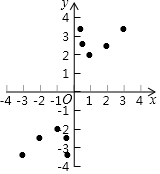 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是x≠0;
(2)如表是y与x的几组对应数值:
在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)进一步探究发现:该函数在第一象限内的最低点的坐标是(1,2),观察函数图象,写出该函数的另一条性质x>1时,y随x增大而增大;0<x<1时,y随x增大而减小;
(4)请你利用配方法证明:当x>0时,y=x+$\frac{1}{x}$的最小值为2.(提示:当x>0时x=($\sqrt{x}$)2,$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2)
 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:(1)自变量x的取值范围是x≠0;
(2)如表是y与x的几组对应数值:
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
(3)进一步探究发现:该函数在第一象限内的最低点的坐标是(1,2),观察函数图象,写出该函数的另一条性质x>1时,y随x增大而增大;0<x<1时,y随x增大而减小;
(4)请你利用配方法证明:当x>0时,y=x+$\frac{1}{x}$的最小值为2.(提示:当x>0时x=($\sqrt{x}$)2,$\frac{1}{x}$=($\frac{1}{\sqrt{x}}$)2)
19.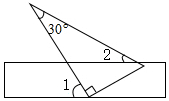 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )
 如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )
如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上.若∠1=55°,则图中∠2的大小为( )| A. | 25° | B. | 30° | C. | 35° | D. | 15° |
4. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
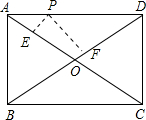 如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB、BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )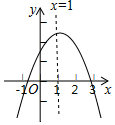 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的交点(x1,0),(x2,0),且-1<x1<0<x2,有下列5个结论:①abc<0;②b>a+c;③a+b>k(ka+b)(k为常数,且k≠1);④2c<3b;⑤若抛物线顶点坐标为(1,n),则b2=4a(c-n),其中正确的结论有( )个.