��Ŀ����
17��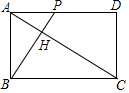 ��ͼ����֪����ABCD�У�AB=2��AD=2$\sqrt{3}$������P�ӵ�A�������յ�D�˶�����BP��������C��CH��BP������ΪH���ٵ�H�������ھ���ABCD֮�⣻��AH����СֵΪ$\sqrt{7}$-$\sqrt{3}$�������˶������У�BPɨ�������ʼ�յ���CHɨ��������������˶������У���H���˶�·�ߣ��켣����Ϊ$\frac{2}{3}$$\sqrt{3}$�У���ȷ���У�����ţ��٢ڢܣ�
��ͼ����֪����ABCD�У�AB=2��AD=2$\sqrt{3}$������P�ӵ�A�������յ�D�˶�����BP��������C��CH��BP������ΪH���ٵ�H�������ھ���ABCD֮�⣻��AH����СֵΪ$\sqrt{7}$-$\sqrt{3}$�������˶������У�BPɨ�������ʼ�յ���CHɨ��������������˶������У���H���˶�·�ߣ��켣����Ϊ$\frac{2}{3}$$\sqrt{3}$�У���ȷ���У�����ţ��٢ڢܣ�
���� ���ݵ�H���˶�·�ߣ��켣��Ϊ��OΪԲ�ĵ�$\widehat{BQ}$�����ɵó���H�������ھ���ABCD֮�⣻���ݵ�A��H��O��ͬһֱ����ʱ��AH��̣����ɵó�AH����Сֵ������BPɨ�������=��ABD�������CHɨ�������=�ȱߡ�COQ�����+����BOQ����������ɵó�BPɨ�������������CHɨ������������ݵ�H���˶�·�ߣ��켣��Ϊ$\widehat{BQ}$�����û������㹫ʽ���ɵó������
��� 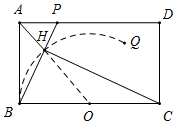 �⣺��ͼ��ʾ����CH��BP��H��
�⣺��ͼ��ʾ����CH��BP��H��
���BHC=90�㣬
���H���˶�·�ߣ��켣��Ϊ��OΪԲ�ĵ�$\widehat{BQ}$��
��OH=OB=$\sqrt{3}$��AB=2��
��OH��AB��
���H�������ھ���ABCD֮�⣬�ʢ���ȷ��
����AH��AO��HO����AH+HO��AO��
�൱A��H��O��ͬһֱ����ʱ��AH��̣�
��ʱAH=AO-HO=$\sqrt{{2}^{2}+��\sqrt{3}��^{2}}$-$\sqrt{3}$��
��AH����СֵΪ$\sqrt{7}$-$\sqrt{3}$���ʢ���ȷ��
����ͼ��ʾ�����˶������У�BPɨ�������=��ABD�����=$\frac{1}{2}$AB��AD=$\frac{1}{2}$��2��2$\sqrt{3}$=2$\sqrt{3}$��
CHɨ�������=�ȱߡ�COQ�����+����BOQ�����=$\frac{\sqrt{3}}{4}$����$\sqrt{3}$��2+$\frac{120���С���\sqrt{3}��^{2}}{360}$=$\frac{3}{4}\sqrt{3}$+�У�
��BPɨ�������������CHɨ����������ʢ۴���
�����˶������У���H���˶�·�ߣ��켣����Ϊ$\widehat{BQ}$=$\frac{120���С�\sqrt{3}}{180}$=$\frac{2}{3}$$\sqrt{3}$�У��ʢ���ȷ��
�ʴ�Ϊ���٢ڢܣ�
���� ������Ҫ�����˹켣�Լ����ε����ʵ����ã�����ʱע�⣺ֱ�����Ե�Բ�ܽ�Ϊֱ�ǣ��������Ĺؼ������ջ����ļ��㹫ʽ�Լ����ε�������㹫ʽ�����ã�

| A�� | 3x+2y=5��x+y�� | B�� | x+x3=x4 | C�� | x2•x3=x6 | D�� | ��x2��3=x6 |
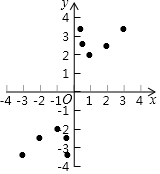 ij�ࡰ��ѧ��ȤС�顱�Ժ���y=x+$\frac{1}{x}$��ͼ������ʽ�����̽����̽���������£��벹��������
ij�ࡰ��ѧ��ȤС�顱�Ժ���y=x+$\frac{1}{x}$��ͼ������ʽ�����̽����̽���������£��벹����������1���Ա���x��ȡֵ��Χ��x��0��
��2�������y��x�ļ����Ӧ��ֵ��
| ��x | �� | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | ��1 | ��2 | ��3 | �� |
| ��y | �� | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | ��$\frac{10}{3}$ | �� |
��3����һ��̽�����֣��ú����ڵ�һ�����ڵ���͵�������ǣ�1��2�����۲캯��ͼ��д���ú�������һ������x��1ʱ��y��x���������0��x��1ʱ��y��x�������С��
��4�����������䷽��֤������x��0ʱ��y=x+$\frac{1}{x}$����СֵΪ2������ʾ����x��0ʱx=��$\sqrt{x}$��2��$\frac{1}{x}$=��$\frac{1}{\sqrt{x}}$��2��
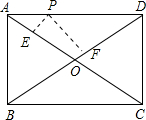 ��ͼ����P�Ǿ���ABCD�ı�AD�ϵ�һ���㣬���ε�������AB��BC�ij��ֱ���6��8�����P�����ε������Խ��߾���֮��PE+PF�ǣ�������
��ͼ����P�Ǿ���ABCD�ı�AD�ϵ�һ���㣬���ε�������AB��BC�ij��ֱ���6��8�����P�����ε������Խ��߾���֮��PE+PF�ǣ�������