题目内容
14．已知：如图1，⊙O与射线MN相切于点M，⊙O的半径为2，AC是⊙O的直径，A与M重合，△ABC是⊙O的内接三角形，且∠C=30°，求弦AB和$\widehat{AB}$的长度；（结果保留π）探究：如图2，若⊙O和△ABC沿射线MN方向作无滑动的滚动，
（1）点B第一次在射线MN上时，圆心O所走过的路线的长；
（2）点B第二次在射线MN上时，圆心O所走过的路线的长．（结果保留π）
分析 探究：（1）利用弧长公式分别求出O点所走过的路线即可；
（2）利用弧长公式分别求出O点所走过的路线即可；
解答 解：探究一：（1）点B第一次在射线MN上时，圆心O所走过的路线的长为$\widehat{AB}$的长度为：$\frac{60π×2}{180}$=$\frac{2}{3}$π，
（2）点B第二次在射线MN上时，圆心O所走过的路线的长为：$\frac{2}{3}$π+2π×2；
点评 此题轨迹，主要考查了弧长公式的应用，本题关键是理解顶点O经过的路线可得．
练习册系列答案
相关题目
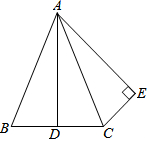已知：如图，△ABC中，AB=AC，AD平分∠BAC，CE⊥AE于E，E在△ABC外，且CE=$\frac{1}{2}$BC．求证：∠ACE=∠B．
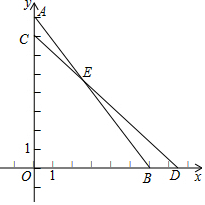以Rt△OAB的两直角边所在的直线为坐标轴，以直角顶点O为原点，建立直角坐标系，如图所示，且点A、B的坐标分别为（0，8）和（6，0）．若保持线段AB的长度不变，点A在y轴正半轴上向下滑动，则点B在x轴正半轴上向右滑动．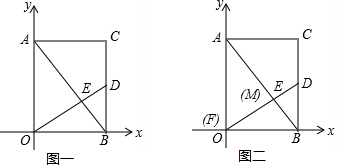
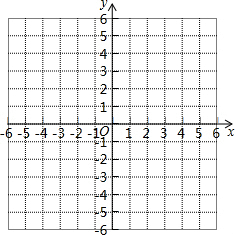已知点A（1，1），B（-1，3），C（-3，1），在坐标系中画出△ABC，并作出△ABC关于x轴的对称图形△A′B′C′，并求△ABC 的面积．