题目内容
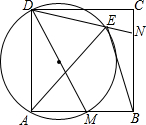 如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.
如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.(1)试证明△ADE△≌ABE;
(2)试探索∠BEN与∠ADM之间的数量关系,并说明理由.
考点:全等三角形的判定与性质,正方形的性质,圆周角定理
专题:
分析:(1)连接ME,可证∠DAE=∠BAE,即可证明△ADE△≌△ABE;
(2)根据外角等于不相邻两内角和即可解题.
(2)根据外角等于不相邻两内角和即可解题.
解答:(1)证明:连接ME,
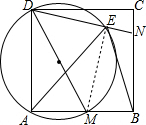
在正方形ABCD中,AD=AB,
∵DM为直径,
∴∠DEM=90°,
∵∠MDN=45°,
∴∠MDE=∠DME=45°,
∵∠DAE=∠DME,∠EAB=∠MDE,
∴∠DAE=∠BAE,
在△ADE△与△ABE中,
,
∴△ADE△≌△ABE(SAS).
(2)解:∵∠ADM=180°-90°-∠DAM=90°-∠DMA,∠DMA=∠AED,
∴∠ADM=90°-∠AED,
∵∠DEA=∠AEB,
∴∠BEN=180°-∠DEA-∠AEB=180°-2∠AED,
∴∠BEN=2∠ADM.

在正方形ABCD中,AD=AB,
∵DM为直径,
∴∠DEM=90°,
∵∠MDN=45°,
∴∠MDE=∠DME=45°,
∵∠DAE=∠DME,∠EAB=∠MDE,
∴∠DAE=∠BAE,
在△ADE△与△ABE中,
|
∴△ADE△≌△ABE(SAS).
(2)解:∵∠ADM=180°-90°-∠DAM=90°-∠DMA,∠DMA=∠AED,
∴∠ADM=90°-∠AED,
∵∠DEA=∠AEB,
∴∠BEN=180°-∠DEA-∠AEB=180°-2∠AED,
∴∠BEN=2∠ADM.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ADE△≌△ABE是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
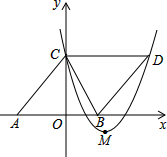 如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为
如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为 如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长.
如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长.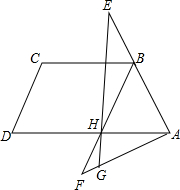 如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=
如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=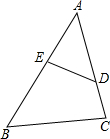 若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为
若∠ADE=∠B,AD=6,AB=12,DE=5,则BC的长为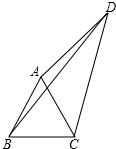 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为
如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为 某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?
某市承办一项大型比赛,在市内有三个体育馆承接所有比赛,现要修建一个运动员公寓,使得运动员公寓到三个体育馆的距离相等,若三个体育馆的位置如图所示,那么运动员公寓应建立在何处?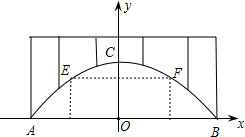 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图,以水面AB所在直线为x轴,AB中点O为原点,建立平面直角坐标系.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)