题目内容
 如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长.
如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长.考点:翻折变换(折叠问题)
专题:
分析:首先根据勾股定理求出EF的长度;然后证明△AEF∽△BGE,列出关于△BGE的三边长的比例式,求出三边的长度即可解决问题.
解答: 解:由题意得:EF=DF(设为x),
解:由题意得:EF=DF(设为x),
则AF=6-x;而AE=3,
由勾股定理得:
x2=32+(6-x)2,
解得:x=
;
AF=6-
=
;
由题意得:
∠GEF=∠D=90°,∠A=∠B=90°,
∴∠AEF+∠AFE=∠AEF+∠BEG,
∴∠AFE=∠BEG;
∴△AEF∽△BGE,
∴
=
=
,
∴EG=
=5,BG=
=4,
∴△EBG的周长=5+4+3=12.
 解:由题意得:EF=DF(设为x),
解:由题意得:EF=DF(设为x),则AF=6-x;而AE=3,
由勾股定理得:
x2=32+(6-x)2,
解得:x=
| 15 |
| 4 |
AF=6-
| 15 |
| 4 |
| 9 |
| 4 |
由题意得:
∠GEF=∠D=90°,∠A=∠B=90°,
∴∠AEF+∠AFE=∠AEF+∠BEG,
∴∠AFE=∠BEG;
∴△AEF∽△BGE,
∴
| EF |
| EG |
| AF |
| BE |
| AE |
| BG |
∴EG=
| ||
|
| 3×3 | ||
|
∴△EBG的周长=5+4+3=12.
点评:该命题考查了翻折变换及其应停用问题;首先根据勾股定理求出EF的长度;然后证明△AEF∽△BGE,借助相似三角形的性质即可求出边长;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
 如图,化简|a+b|-|a|+|b|=
如图,化简|a+b|-|a|+|b|= (1)画出图1中△ABC关于直线L的对称图形△A′B′C′.
(1)画出图1中△ABC关于直线L的对称图形△A′B′C′.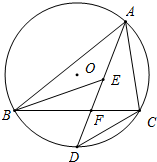 如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.
如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.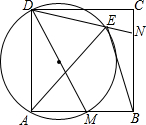 如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.
如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.