题目内容
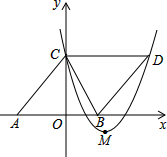 如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为
如图,在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,顶点C在y轴上,A(-6,0),C(0,8),抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,则抛物线解析式为考点:菱形的性质,待定系数法求二次函数解析式
专题:
分析:由在平面直角坐标系xOy中,菱形ABDC的边AB在x轴上,A(-6,0),C(0,8),利用勾股定理即可求得AC的长,继而求得点B坐标,继而求得直线BC的解析式,然后由抛物线y=ax2-10ax+c经过点C,且顶点M在直线BC上,求得答案.
解答:解:∵A(-6,0),C(0,8),
∴OA=6,OC=8,
∴AC=
=10,
∵四边形ABCD是菱形,
∴AB=CD=AC=10,
∴OB=AB-OA=4,
∴点B(4,0),
设直线BC的解析式为:y=kx+b,
,
解得:
,
∴直线BC的解析式为:y=-2x+8,
∵抛物线y=ax2-10ax+c经过点C,
∴c=8,
∴x=-
=5,y=
=8-25a,
∴顶点为:(5,8-25a),
∵顶点M在直线BC上,
∴8-25a=-2×5+8,
∴a=
,
∴抛物线解析式为:y=
x2-4x+8.
故答案为:y=
x2-4x+8.
∴OA=6,OC=8,
∴AC=
| OA2+OC2 |
∵四边形ABCD是菱形,
∴AB=CD=AC=10,
∴OB=AB-OA=4,
∴点B(4,0),
设直线BC的解析式为:y=kx+b,
|
解得:
|
∴直线BC的解析式为:y=-2x+8,
∵抛物线y=ax2-10ax+c经过点C,
∴c=8,
∴x=-
| -10a |
| 2a |
| 4ac-(-10a)2 |
| 4a |
∴顶点为:(5,8-25a),
∵顶点M在直线BC上,
∴8-25a=-2×5+8,
∴a=
| 2 |
| 5 |
∴抛物线解析式为:y=
| 2 |
| 5 |
故答案为:y=
| 2 |
| 5 |
点评:此题考查了菱形的性质、待定系数法求函数的解析式以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 据绝对值的几何意义,方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值.在数轴上,1和-2的距离之和为3,所以满足方程的x的对应点在1的右边或-2的左边;若x对应点在1的右边,由图可看出x=2;同时,若x对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.
据绝对值的几何意义,方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值.在数轴上,1和-2的距离之和为3,所以满足方程的x的对应点在1的右边或-2的左边;若x对应点在1的右边,由图可看出x=2;同时,若x对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3. 如图,化简|a+b|-|a|+|b|=
如图,化简|a+b|-|a|+|b|= 已知:如图,抛物线y=ax2+bx+c经过A(1,0),B(5,0),C(0,5)三点.
已知:如图,抛物线y=ax2+bx+c经过A(1,0),B(5,0),C(0,5)三点.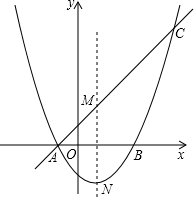 如图,抛物线y=
如图,抛物线y=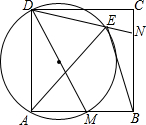 如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.
如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.