题目内容
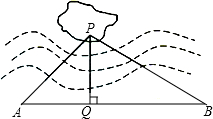 如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(
如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:AB=100米,∠PAB=45°,∠PBA=30.请求出小桥PQ的长.(| 2 |
| 3 |
考点:解直角三角形的应用
专题:
分析:设PQ=x米,在直角△PAQ和直角△PBQ中分别利用x表示出AQ和BQ的长,根据AB=AQ+BQ,即可列方程求得x的值.
解答:解:设PQ=x米,
在直角△PAQ中,tan∠PAQ=
,
∴AQ=
=x,
在直角△PBQ中,tan∠PBQ=
,
∴BQ=
=
x,
∵AB=100米,
∴x+
x=100,
解得:x=50
-50≈36.6(米).
答:小桥PQ的长度约是36.6米.
在直角△PAQ中,tan∠PAQ=
| x |
| AQ |
∴AQ=
| x |
| tan45° |
在直角△PBQ中,tan∠PBQ=
| x |
| BQ |
∴BQ=
| x |
| tan30° |
| 3 |
∵AB=100米,
∴x+
| 3 |
解得:x=50
| 3 |
答:小桥PQ的长度约是36.6米.
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度,难度一般.

练习册系列答案
相关题目
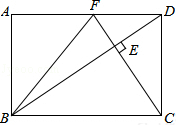 在矩形ABCD中,DC=
在矩形ABCD中,DC= 如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN.
如图,在Rt△ABC中,∠C=90°,以边AC为直径作⊙O,与斜边AB交于点M,点N是边BC的中点,连接MN. 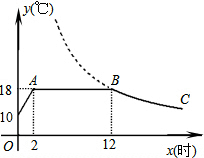 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培蔬菜.图中是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=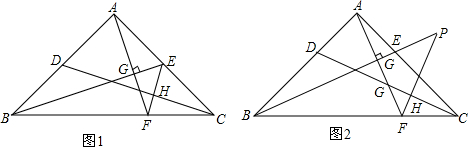
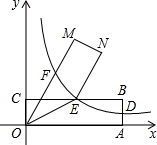 如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=c,在移动过程中,双曲线y=
如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=c,在移动过程中,双曲线y=