题目内容
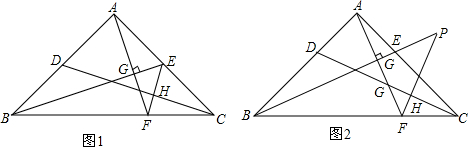
 如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.(1)求证:△ABD≌△CAE;
(2)若∠FBA=60°,连接DF、EF,判断△DEF的形状,并说明理由.
考点:菱形的性质,全等三角形的判定与性质,等腰三角形的判定
专题:
分析:(1)利用菱形的性质得出AB=AC,进而得出∠2=∠3,即可利用AAS证明△ABD≌△CAE;
(2)易证△ABF与△ACF均为等边三角形,然后证明△FBD≌△FAE,则DF=EF,∠BFD=∠AFE,从而求得∠DFE的度数,即可证得:△DEF是等边三角形.
(2)易证△ABF与△ACF均为等边三角形,然后证明△FBD≌△FAE,则DF=EF,∠BFD=∠AFE,从而求得∠DFE的度数,即可证得:△DEF是等边三角形.
解答:(1)证明:∵四边形ABFC为菱形,
∴AB=AC.
∵∠BDA=∠BAC=∠CEA,
又∵∠2+∠1=180°-∠BDA,∠3+∠1=180°-∠BAC,
∴∠2=∠3.
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS);
(2)答:△DEF是等边三角形.
解:连结AF,
∵四边形ABFC为菱形,∠FBA=60°,
∴△ABF与△ACF均为等边三角形,
∴BF=AF,∠FBA=∠FAC=60°=∠BFA.
∵∠2=∠3,
∴∠FBA+∠2=∠FAC+∠3,即∠FBD=∠FAE,
∵△ABD≌△CAE,
∴BD=AE.
在△FBD和△FAE中,
,
∴△FBD≌△FAE,
∴DF=EF,∠BFD=∠AFE.
∵∠BFA=∠BFD+∠DFA=60°,
∴∠AFE+∠DFA=60°,即∠DFE=60°.
∴△DEF是等边三角形.
∴AB=AC.
∵∠BDA=∠BAC=∠CEA,
又∵∠2+∠1=180°-∠BDA,∠3+∠1=180°-∠BAC,
∴∠2=∠3.
在△ABD和△CAE中,

|
∴△ABD≌△CAE(AAS);
(2)答:△DEF是等边三角形.
解:连结AF,
∵四边形ABFC为菱形,∠FBA=60°,
∴△ABF与△ACF均为等边三角形,
∴BF=AF,∠FBA=∠FAC=60°=∠BFA.
∵∠2=∠3,
∴∠FBA+∠2=∠FAC+∠3,即∠FBD=∠FAE,
∵△ABD≌△CAE,
∴BD=AE.
在△FBD和△FAE中,
|
∴△FBD≌△FAE,
∴DF=EF,∠BFD=∠AFE.
∵∠BFA=∠BFD+∠DFA=60°,
∴∠AFE+∠DFA=60°,即∠DFE=60°.
∴△DEF是等边三角形.
点评:本题考查了全等三角形的判定与性质以及菱形的性质,正确作出辅助线是关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
下列平面图形中,不是正方体的表面展开图的是( )
A、 |
B、 |
C、 |
D、 |
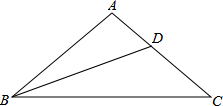 问题:在△ABC中,AB=AC,∠A=100°,BD为∠B的平分线,探究AD、BD、BC之间的数量关系.
问题:在△ABC中,AB=AC,∠A=100°,BD为∠B的平分线,探究AD、BD、BC之间的数量关系.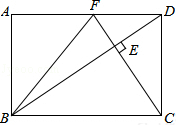 在矩形ABCD中,DC=
在矩形ABCD中,DC= 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:
如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证: