题目内容
16.某老师给同学们送甲、乙两种新年贺卡,已知甲、乙两种贺卡的单价分别是8元和10元,现需购买这两种贺卡共36张.且购买甲种贺卡的数量不超过乙种贺卡数量的2倍,设购买甲种贺卡x张,购买两种贺卡的总费用为y元.(1)求y关于自变量x的函数表达式.
(2)当x为多少时,总费用最少?最少的费用是多少元?
分析 (1)根据总费用=购买甲、乙两种贺卡的费用之和,即可解决问题,再列出不等式确定自变量的取值范围即可.
(2)利用一次函数的增减性即可解决问题.
解答 解:(1)由题意y=8x+10(36-x)=-2x+360,
∵0≤x≤36-x,
∴0≤x≤18,
(2)∵y=-2x+360,-2<0
∴y随x的增加而减小,
∴x=18时,y最小,最小费用为324元.
点评 本题考查一次函数的应用、一元一次不等式的应用等知识,解题的关键是理解题意,学会构建一次函数解决实际问题,属于中考常考题型.

练习册系列答案
相关题目
6.数轴上表示-6的点和表示2016的点之间的距离是( )
| A. | 2010 | B. | 2022 | C. | -2022 | D. | -2010 |
7.观察如图,并阅读图形下面的相关文字:

像这样,20条直线相交,交点最多的个数是( )

像这样,20条直线相交,交点最多的个数是( )
| A. | 100个 | B. | 135个 | C. | 190个 | D. | 200个 |
4.若x=2是关于x的方程mx+2=3(m-x)的解,则m的值是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
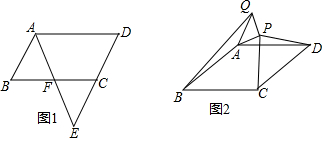
11. 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )| A. | 1cm | B. | 2cm | C. | $\frac{\sqrt{6}}{2}$cm | D. | $\sqrt{3}$cm |
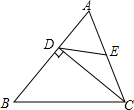 如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.
如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.