题目内容
11. 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )| A. | 1cm | B. | 2cm | C. | $\frac{\sqrt{6}}{2}$cm | D. | $\sqrt{3}$cm |
分析 首先作QH⊥PA,垂足为H,则QH=2cm,易证得△APQ为等边三角形,然后利用三角函数即可求得PQ的长.
解答 解:如图,作QH⊥PA,垂足为H,则QH=$\sqrt{3}$cm,
由平行线的性质,得∠DPA=∠BAC=60°,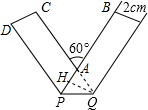
由折叠的性质,得∠DPQ+∠APQ=180°,
即∠DPA+∠APQ+∠APQ=180°,60°+2∠APQ=180°,
∴∠APQ=60°,
又∵∠PAQ=∠BAC=60°,
∴△APQ为等边三角形,
在Rt△PQH中,sin∠HPQ=$\frac{QH}{QP}$,
∴QP=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2cm.
故选B.
点评 此题考查了翻折变换、等边三角形的判定与性质、特殊角的三角函数等知识,证得△APQ为等边三角形是解此题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
2. 在图中的数轴上,表示-$\frac{1}{3}$的是( )
在图中的数轴上,表示-$\frac{1}{3}$的是( )
 在图中的数轴上,表示-$\frac{1}{3}$的是( )
在图中的数轴上,表示-$\frac{1}{3}$的是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
19. 图中数轴的单位长度为1,如果已知点A、点C表示的数是互为相反数,那么点D表示的数是( )
图中数轴的单位长度为1,如果已知点A、点C表示的数是互为相反数,那么点D表示的数是( )
 图中数轴的单位长度为1,如果已知点A、点C表示的数是互为相反数,那么点D表示的数是( )
图中数轴的单位长度为1,如果已知点A、点C表示的数是互为相反数,那么点D表示的数是( )| A. | -1 | B. | -2 | C. | 2 | D. | 5 |
6.下列解方程过程中,变形正确的是( )
| A. | 由x+5=6x-7得5x=5-7 | B. | 由-2(x-1)=3得-2x-2=3 | ||
| C. | 由$\frac{x-3}{0.7}$=1得$\frac{10x-30}{7}$=10 | D. | 由$\frac{1}{2}$x+9=-$\frac{3}{2}$x-3得2x=-12 |
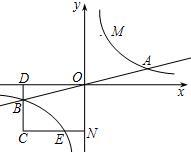 已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点,第一象限上的点M(m,n)(在A点左侧)是双曲线的动点,过点B作BD∥于y轴于点D,过N(-,-n)作NC∥x轴交双曲线于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为y=$\frac{2}{3}$x+$\frac{2}{3}$.
已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点,第一象限上的点M(m,n)(在A点左侧)是双曲线的动点,过点B作BD∥于y轴于点D,过N(-,-n)作NC∥x轴交双曲线于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为y=$\frac{2}{3}$x+$\frac{2}{3}$.