题目内容
13.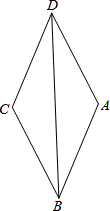 如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.
如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.(1)当⊙O经过点A时,用尺规作图作出⊙O;此时,点C在⊙O上吗?为什么?
(2)当⊙O与AB相切于点A时,
①求证:BC与⊙O相切;
②若OB=1,⊙O的面积=$\frac{π}{4}$.
分析 (1)如图1,作AD的垂直平分线MN交BD于O,以O为圆心,OD为半径作⊙O,则⊙O即为所求,由菱形的性质得到边角的关系,通过三角形全等得到结论.
(2)①由三角形全等得到对应角相等,证得垂直得到BC与⊙O相切;
②解直角三角形得到半径的长度,由圆的面积公式求得.
解答  解:如图1(1)作AD的垂直平分线MN 交BD于O,以O为圆心,OD为半径作⊙O,
解:如图1(1)作AD的垂直平分线MN 交BD于O,以O为圆心,OD为半径作⊙O,
则⊙O即为所求;
点C 在圆上,
理由如下;
∵四边形ABCD是菱形,
∴CD=DA,∠CDB=∠ADB,
在△CDO与△ADO中,
$\left\{\begin{array}{l}{CD=AD}\\{∠CDO=ADO}\\{OD=OD}\end{array}\right.$,
∴△CDO≌△ADO,
∴OC=OA,
∴点C在⊙O上;
(2)①当⊙O与AB相切于点A时,
∠OAB=90°,
在△ABO与△BCO中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABO=∠BCO}\\{OB=OB}\end{array}\right.$,
∴△ABO≌△BCO,
∴∠BCO=∠BAO=90°,
∴BC⊥OC,
∴BC与⊙O相切;
②∵∠CDA=∠ABC=$\frac{1}{2}$∠AOC,
∴∠ABC=60°,
∴∠CBO=30°,
∵OB=1,
∴OC=$\frac{1}{2}$OB=$\frac{1}{2}$,
∴⊙O的面积=${(\frac{1}{2})}^{2}$•π=$\frac{π}{4}$.
点评 本题考查了尺规作图,全等三角形的判定与性质,直线与圆的位置关系,圆面积的求法,正确的作出图形是解题的关键.

练习册系列答案
相关题目
3.已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
| 注入水的时间t(分钟) | 0 | 10 | … | 25 |
| 水池的容积V(公升) | 100 | 300 | … | 600 |
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
18. 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )| A. | 从图中可以直接看出喜欢各种球类的具体人数 | |
| B. | 从图中可以直接看出全班的总人数 | |
| C. | 从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 | |
| D. | 从图中可以直接看出全班同学现在喜欢各种球类人数的大小关系 |
5.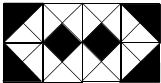 甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )
甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )
 甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )
甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )| A. | 甲大 | B. | 乙大 | C. | 相等 | D. | 不确定 |
 如图,在四边形ABCD中,AD∥BC,AB=AC,BE=CE=AD.
如图,在四边形ABCD中,AD∥BC,AB=AC,BE=CE=AD.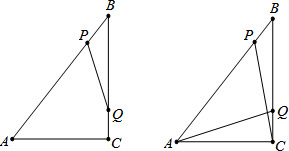
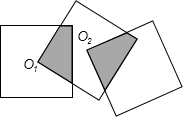 如图,三个边长均为4的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,则阴影部分面积是8.
如图,三个边长均为4的正方形重叠在一起,O1,O2是其中两个正方形的对角线交点,则阴影部分面积是8.