题目内容
1.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值;
(3)M是PQ的中点,请直接写出点M运动路线的长.
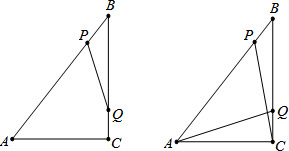
分析 (1)分两种情况:①当△BPQ∽△BAC时,BP:BA=BQ:BC;当△BPQ∽△BCA时,BP:BC=BQ:BA,再根据BP=5t,QC=4t,AB=10cm,BC=8cm,代入计算即可;
(2)过P作PF⊥BC于点F,AQ,CP交于点N,则有PB=5t,PF=3t,FC=8-4t,根据△ACQ∽△CFP,得出AC:CF=CQ:FP,代入计算即可.
(3)作PE⊥AC于点E,MH⊥AC于点H,先得出MH=$\frac{PE+QC}{2}$,再把QC=4t,PE=8-CF=8-4t代入求出MH,过BC的中点R作直线平行于AC,得出RC=MH,M在过R的中位线上,从而证出PQ的中点在△ABC的一条中位线上.
解答 解:根据勾股定理得:BA=$\sqrt{{6}^{2}+{8}^{2}}$;
(1)分两种情况讨论:
①当△BPQ∽△BAC时,$\frac{BP}{BA}$=$\frac{BQ}{BC}$,
∵BP=5t,QC=4t,AB=10,BC=8,
∴$\frac{5t}{10}$=$\frac{8-4t}{8}$,解得,t=1;
②当△BPQ∽△BCA时,$\frac{BP}{BC}$=$\frac{BQ}{BA}$,
∴$\frac{5t}{8}$=$\frac{8-4t}{10}$,解得,t=$\frac{32}{41}$;
∴t=1或$\frac{32}{41}$时,△BPQ∽△BCA;
(2)过P作PF⊥BC于点F,AQ,CP交于点N,如答图1所示:
则PB=5t,PF=3t,FC=8-4t,
∵∠NAC+∠NCA=90°,∠PCF+∠NCA=90°,
∴∠NAC=∠PCF,
∵∠ACQ=∠PFC,
∴△ACQ∽△CFP,
∴$\frac{AC}{CF}$=$\frac{CQ}{FP}$,
∴$\frac{4t}{3t}$=$\frac{6}{8-4t}$,解得t=$\frac{7}{8}$.
(3)点M运动路线的长是3cm.理由如下:
如答图2,连接PQ.仍有PF⊥BC于点F,PQ的中点设为M点,再作PE⊥AC于点E,DH⊥AC于点H, ∵∠ACB=90°,
∵∠ACB=90°,
∴MH为梯形PECQ的中位线,
∴MH=$\frac{PE+QC}{2}$,
∵QC=4t,PE=8-BF=8-4t,
∴MH=$\frac{8-4t+4t}{2}$=4,
∵BC=8,过BC的中点R作直线平行于AC,
∴RC=MH=4成立,
∴M在过R的中位线上,
∴PQ的中点M在△ABC的一条中位线上运动,
∴点M的运动轨迹是△ABC的中位线,其长度为:$\frac{1}{2}$AC=$\frac{1}{2}$×6=3(cm).
点评 此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、中位线的性质等,关键是画出图形作出辅助线构造相似三角形,注意分两种情况讨论.

| A. | 5 | B. | 6 | C. | 7 | D. | 5或6或7 |
| A. | $\frac{3\sqrt{3}}{2}$a2 | B. | 6a2 | C. | $\frac{\sqrt{3}}{4}$a2 | D. | 3$\sqrt{3}$a2 |
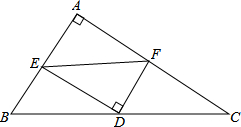 如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )
如图,在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.若BE=2,CF=3,则EF的值可能为( )| A. | 7 | B. | 6 | C. | 5 | D. | $\sqrt{13}$ |
 如图,等腰△ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.
如图,等腰△ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长. 已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,将线段AB平移至DE,连接AE、AD、EC. 如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.
如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.