题目内容
3.已知m、n为实数,且m=$\sqrt{{n}^{2}-9}$+$\sqrt{9-{n}^{2}}$+4,则m-n=7或1.分析 直接利用二次根式有意义的条件进而得出m,n的值即可得出答案.
解答 解:由题意得:m=$\sqrt{{n}^{2}-9}$+$\sqrt{9-{n}^{2}}$+4,则n=±3,m=4,
故m-n=4±3=7或1.
故答案为:7或1.
点评 此题主要考查了二次根式有意义的条件,得出m,n的值是解题关键.

练习册系列答案
相关题目
8.下列计算正确的是( )
| A. | (a+6)(a-6)=a2-12 | B. | (x+5)(x-6)=x2-30 | ||
| C. | (a+1)2=a2+1 | D. | (-5xy-2)(2-5xy)=25x2y2-4 |
15. 实数a在数轴上的位置如图所示,则下列说法不正确的是( )
实数a在数轴上的位置如图所示,则下列说法不正确的是( )
 实数a在数轴上的位置如图所示,则下列说法不正确的是( )
实数a在数轴上的位置如图所示,则下列说法不正确的是( )| A. | a的相反数大于2 | B. | a的相反数是2 | C. | |a|>2 | D. | 2a<0 |
12.已知点M(4,2),N(1,1),点P是x轴上一动点,若使PM+PN最短,则点P为( )
| A. | (2,0) | B. | (2.5,0) | C. | (3,0) | D. | (4,0) |
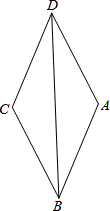 如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O.
如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为⊙O. 如图,矩形ABCD中,AB=12cm,BC=25cm,E是AD上一点,且AE:ED=16:9.试判断∠BEC是否为直角,并说明理由.
如图,矩形ABCD中,AB=12cm,BC=25cm,E是AD上一点,且AE:ED=16:9.试判断∠BEC是否为直角,并说明理由.