题目内容
15.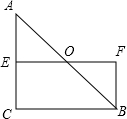 如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC,求证:四边形BCEF是矩形.
如图,在Rt△ABC中,∠C=90°,O是斜边AB上的中点,AE=CE,BF∥AC,求证:四边形BCEF是矩形.
分析 根据题意易正明△AOE≌△BOF,得BF=AE,即可得出CE=BF,可证明四边形BCEF是平行四边形,根据∠C=90°,根据一个角为直角的平行四边形为矩形,即可得出四边形BCEF是矩形.
解答 证明:∵O是AB中点,BF∥AC,
∴∠A=∠OBF,OA=OB,
在△AOE和△BOF中,
$\left\{\begin{array}{l}{∠A=∠OBF}\\{OA=OB}\\{∠AOE=∠BOF}\end{array}\right.$,
∴△AOE≌△BOF,
∴BF=AE,
又∵AE=CE,
∴CE=BF,
又∵CE∥BF,
∴四边形BCEF是平行四边形,
又∵∠C=90°,
∴四边形BCEF是矩形.
点评 本题考查了矩形的判定以及平行四边形的判定方法,掌握有一个角为直角的平行四边形为矩形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列命题中,假命题是( )
| A. | 对角线互相垂直平分的四边形是矩形 | |
| B. | 邻角相等的菱形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 一组邻边相等的平行四边形是菱形 |
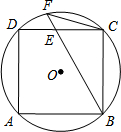 如图,⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,则弦FC的长为$\frac{\sqrt{10}}{5}$.
如图,⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,则弦FC的长为$\frac{\sqrt{10}}{5}$.

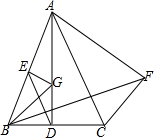 如图,△ABC中,AB=AC,D,E分别是BC,AB的中点,作BF⊥AC且使BF=AC,BG平分∠ABF.
如图,△ABC中,AB=AC,D,E分别是BC,AB的中点,作BF⊥AC且使BF=AC,BG平分∠ABF.